Some Continuous Univariate Probability Distributions
Several continuous PDFs are used frequently in reliability analysis. They include normal, lognormal, gamma, Weibull, and exponential distributions. Other distributions, such as beta and extremal distributions, also are used sometimes.
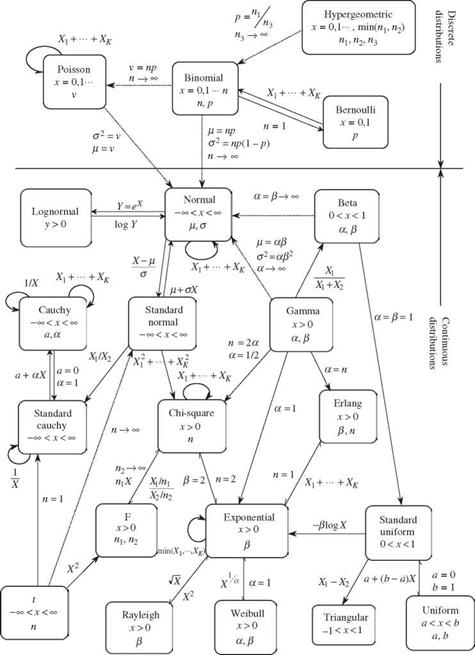
The relations among the various continuous distributions considered in this chapter and others are shown in Fig. 2.15.
1.6.1 Normal (Gaussian) distribution
The normal distribution is a well-known probability distribution involving two parameters: the mean and variance. A normal random variable having the mean /гх and variance a2 is denoted herein as X ~ N (tx, ax) with the PDF
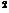
![]()
 fN (x | tx, ax2) = —І— exp ■sj2n ax
fN (x | tx, ax2) = —І— exp ■sj2n ax
The relationship between tx and ax and the L-moments are tx = Л1 and
ax = рЯ^2.
The normal distribution is bell-shaped and symmetric with respect to the mean [ix. Therefore, the skewness coefficient of a normal random variable is zero. Owing to the symmetry of the PDF, all odd-order central moments are zero. Thekurtosis of a normal random variable is kx = 3.0. Referring to Fig. 2.15, a linear function of several normal random variables also is normal. That is, the linear combination of K normal random variables W = a1 X1 + a2X2 + ■ ■ ■ + aKXK, with Xk ~ N(tk, ak), for k = 1, 2,…, K, is also a normal random variable with the mean tw and variance aW, respectively, as
K K K-1 K
t^w У ^ akt^k aw У ^ akak + 2 У ^ У ^ akakCov(Xk, Xk)
k = 1 k = 1 k = 1 k = k+1
The normal distribution sometimes provides a viable alternative to approximate the probability of a nonnormal random variable. Of course, the accuracy of such an approximation depends on how closely the distribution of the nonnormal random variable resembles the normal distribution. An important theorem relating to the sum of independent random variables is the central limit theorem, which loosely states that the distribution of the sum of a number of independent random variables, regardless of their individual distributions, can be approximated by a normal distribution, as long as none of the variables has a dominant effect on the sum. The larger the number of random variables involved in the summation, the better is the approximation. Because many natural processes can be thought of as the summation of a large number of independent component processes, none dominating the others, the normal distribution is a reasonable approximation for these overall processes. Finally, Dowson and Wragg (1973) have shown that when only the mean and variance are specified, the maximum entropy distribution on the interval (-to, +to) is the normal distribution. That is, when only the first two moments are specified, the use of the normal distribution implies more information about the nature of the underlying process specified than any other distributions.
Probability computations for normal random variables are made by first transforming the original variable to a standardized normal variable Z by
|
Z = (X — /лх )/ax
in which Z has a mean of zero and a variance of one. Since Z is a linear function of the normal random variable X, Z is therefore normally distributed, that is, Z ~ N(jaz = 0, az = 1). The PDF of Z, called the standard normal distribution, can be obtained easily as
The general expressions for the product-moments of the standard normal random variable are
where z = (x — их)/aX, and Ф^) is the standard normal CDF defined as
![]() Ф( z) = ф (z) dz
Ф( z) = ф (z) dz
— TO
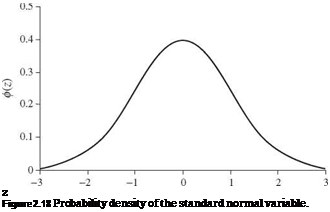
Figure 2.18 shows the shape of the PDF of the standard normal random variable.
 |
The integral result of Eq. (2.62) is not analytically available. A table of the standard normal CDF, such as Table 2.2 or similar, can be found in many statistics textbooks (Abramowitz and Stegun, 1972; Haan, 1977; Blank, 1980;
|
TABLE 2.2 Table of Standard Normal Probability, Ф( z) = P(Z < z)
NOTE: Ф(-г) = 1 – Ф(г), z > 0. |
Devore, 1987). For numerical computation purposes, several highly accurate approximations are available for determining Ф(z). One such approximation is the polynomial approximation (Abramowitz and Stegun, 1972)
Ф(z) = 1 – ф(z)(b1t + b2t2 + b3t3 + b4t4 + b5t5) for z > 0 (2.63)
in which t = 1/(1 + 0.2316419z), b1 = 0.31938153, b2 = -0.356563782, b3 = 1.781477937, b4 = -1.821255978, and b5 = 1.33027443. The maximum absolute error of the approximation is 7.5 x 10-8, which is sufficiently accurate for most practical applications. Note that Eq. (2.63) is applicable to the non-negativevalued z. For z < 0, the value of standard normal CDF can be computed as ФЫ = 1 – Ф(|z|) by the symmetry of ф(z). Approximation equations, such as
Eq. (2.63), can be programmed easily for probability computations without needing the table of the standard normal CDF.
Equally practical is the inverse operation of finding the standard normal quantile zp with the specified probability level p. The standard normal CDF table can be used, along with some mechanism of interpolation, to determine zp. However, for practical algebraic computations with a computer, the following rational approximation can be used (Abramowitz and Stegun, 1972):
in which p = ), t = y/-2 ln(1 – p), c0 = 2.515517, ci = 0.802853, c2 =
0.010328, d1 = 1.432788, d2 = 0.189269, and d3 = 0.001308. The corresponding maximum absolute error by this rational approximation is 4.5 x 10-4. Note that Eq. (2.64) is valid for the value of Ф^) that lies between [0.5, 1]. When p < 0.5, one can still use Eq. (2.64) by letting t = J-2 x ln(p) and attaching a negative sign to the computed quantile value. Vedder (1995) proposed a simple approximation for computing the standard normal cumulative probabilities and standard normal quantiles.
Example 2.16 Referring to Example 2.14, determine the probability of more than five overtopping events over a 100-year period using a normal approximation.
Solution In this problem, the random variable X of interest is the number of overtopping events in a 100-year period. The exact distribution of X is binomial with parameters n = 100 and p = 0.02 or the Poisson distribution with a parameter v = 2. The exact probability of having more than five occurrences of overtopping in 100 years can be computed as
![]()
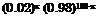
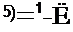
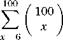
P(X > 5) =
= 1 – 0.9845 = 0.0155
As can be seen, there are a total of six terms to be summed up on the right-hand side. Although the computation of probability by hand is within the realm of a reasonable task, the following approximation is viable. Using a normal probability approximation, the mean and variance of X are
/Px = np = (100)(0.02) = 2.0 al = npq = (100)(0.02)(0.98) = 1.96
The preceding binomial probability can be approximated as
P(X > 6) ^ P(X > 5.5) = 1 – P(X < 5.5) = 1 – P [Z < (5.5 – 2.0)/УЇ96]
= 1 – Ф(2.5) = 1 – 0.9938 = 0.062
DeGroot (1975) showed that when np 1.5 >
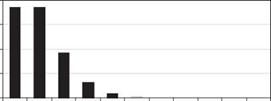
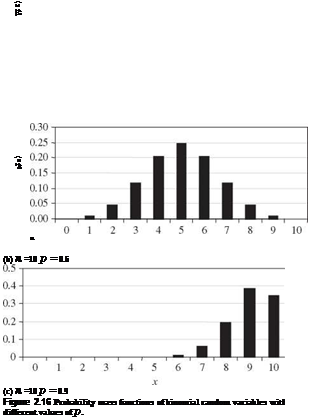
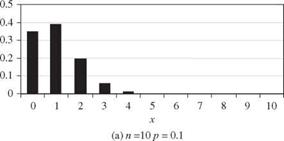
1.07, the error of using the normal distribution to approximate the binomial probability did not exceed 0.05. The error in the approximation gets smaller as the value of np15 becomes larger. For this example, np15 = 0.283 < 1.07, and the accuracy of approximation was not satisfactory as shown.
Example 2.17 (adopted from Mays and Tung, 1992) The annual maximum flood magnitude in a river has a normal distribution with a mean of 6000 ft3/s and standard deviation of 4000 ft3/s. (a) What is the annual probability that the flood magnitude would exceed 10,000 ft3/s? (b) Determine the flood magnitude with a return period of 100 years.
Solution (a) Let Q be the random annual maximum flood magnitude. Since Q has a normal distribution with a mean xq = 6000 ft3/s and standard deviation oq = 4000 ft3/s, the probability of the annual maximum flood magnitude exceeding 10,000 ft3/s is
P(Q > 10, 000) = 1 – P [Z < (10, 000 – 6000)/4000]
= 1 – Ф(1.00) = 1 – 0.8413 = 0.1587
(b) A flood event with a 100-year return period represents the event the magnitude of which has, on average, an annual probability of 0.01 being exceeded. That is, P(Q > 7100) = 0.01, in which 7100 is the magnitude of the 100-year flood. This part of the problem is to determine 7100 from
P(Q < 7100) = 1 – P(Q > 7100) = 0.99
because P(Q < 7100) = P {Z < [(7100 – xq)/oq]}
= P [Z < (7100 – 6000)/4000]
= Ф[71.00 – 6000)/4000] = 0.99
From Table 2.2 or Eq. (2.64), one can find that Ф(2.33) = 0.99. Therefore,
(7100 – 6000)/4000 = 2.33
which gives that the magnitude of the 100-year flood event as 7100 = 15, 320 ft3/s.







 • •
• •


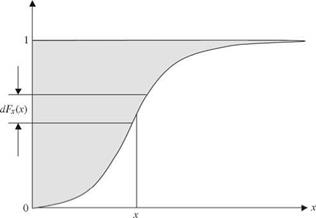
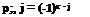 rfr + i (-1)r j (r + j )!
rfr + i (-1)r j (r + j )!![Statistical Properties of Random Variables Подпись: рЖ рЖ E {T [Ft (T )^}= / [t Ft (t)] ft (t) dt = [t(1 - e-t/0 )](e—t/0/0) dt = 40 00](/img/1312/image082_1.png) 01 =
01 =