Skewness coefficient and kurtosis

The asymmetry of the PDF of a random variable is measured by the skewness coefficient Yx, defined as

E [(X — ,x)3]

_ _M3_ Yx = ,,1.5 ^2

(2.40)

a

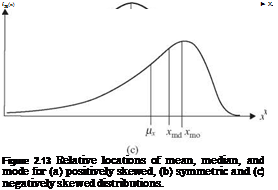
The skewness coefficient is dimensionless and is related to the third-order central moment. The sign of the skewness coefficient indicates the degree of symmetry of the probability distribution function. If yx = 0, the distribution is symmetric about its mean. When yx > 0, the distribution has a long tail to the right, whereas yx < 0 indicates that the distribution has a long tail to the left. Shapes of distribution functions with different values of skewness coeffi­cients and the relative positions of the mean, median, and mode are shown in Fig. 2.13.

Similarly, the degree of asymmetry can be measured by the L-skewness coefficient t3, defined as

тз = A.3/A.2 (2.41)

The value of the L-skewness coefficient for all feasible distribution functions must lie within the interval of [-1, 1] (Hosking, 1986).

Another indicator of the asymmetry is the Pearson skewness coefficient, defined as

l^x xmo

Y1 =————-

®x

As can be seen, the Pearson skewness coefficient does not require computing the third-order moment. In practice, product-moments higher than the third order are used less because they are unreliable and inaccurate when estimated from a small number of samples. Equations used to compute the sample product — moments are listed in the last column of Table 2.1.

Kurtosis kx is a measure of the peakedness of a distribution. It is related to the fourth-order central moment of a random variable as

with kx > 0. For a random variable having a normal distribution (Sec. 2.6.1), its kurtosis is equal to 3. Sometimes the coefficient of excess, defined as ex = kx — 3, is used. For all feasible distribution functions, the skewness coefficient and kurtosis must satisfy the following inequality relationship (Stuart and Ord,

1987)

yX + 1 < Kx

By the definition of L-moments, the L-kurtosis is defined as

T4 = Л4/Л2

Similarly, the relationship between the L-skewness and L-kurtosis for all fea­sible probability distribution functions must satisfy (Hosking, 1986)

Royston (1992) conducted an analysis comparing the performance of sample skewness and kurtosis defined by the product-moments and L-moments. Results indicated that the L-skewness and L-kurtosis have clear advantages

over the conventional product-moments in terms of being easy to interpret, fairly robust to outliers, and less unbiased in small samples.