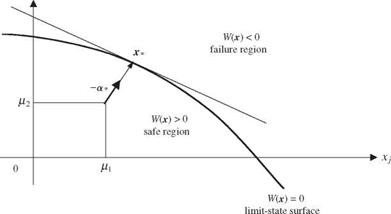
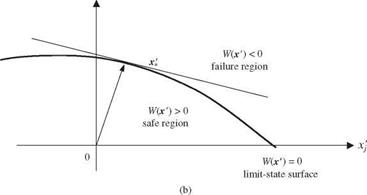
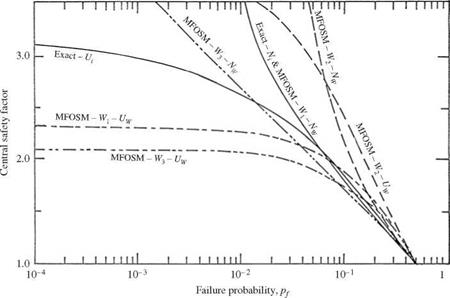
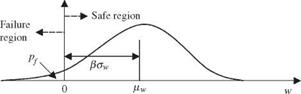
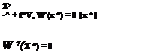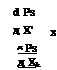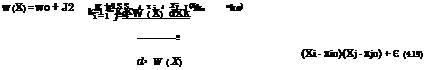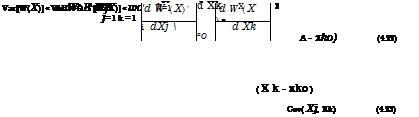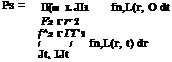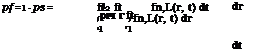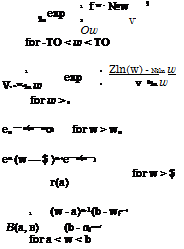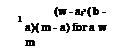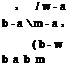Treatment of nonnormal stochastic variables
When nonnormal random variables are involved, it is advisable to transform them into equivalent normal variables. Rackwitz (1976) and Rackwitz and Fiessler (1978) proposed an approach that transforms a nonnormal distribution into an equivalent normal distribution so that the probability content is preserved. That is, the value of the CDF of the transformed equivalent normal distribution is the same as that of the original nonnormal distribution at the design point x*. Later, Ditlvesen (1981) provided the theoretical proof of the convergence property of the normal transformation in the reliability algorithms searching for the design point. Table 4.3 presents the normal equivalent for some nonnormal distributions commonly used in reliability analysis.
By the Rackwitz (1976) approach, the normal transform at the design point x* satisfies the following condition:
Fk (xk-) = ф(Xk – ‘k-N ) = Ф(гІ) for k = 1,2,…, K (4.59)
V ak*N J
in which Fk (xk-) is the marginal CDF of the stochastic basic variable Xk having values at xk-, ‘k-N and ok-N are the mean and standard deviationas of the normal equivalent for the kth stochastic basic variable at Xk = xk-, and zk – = Ф-1[Fk(xk-)] is the standard normal quantile. Equation (4.59) indicates that the marginal probability content in both the original and normal transformed spaces must be preserved. From Eq. (4.59), the following equation is obtained:
‘k-N = xk – – Zk-Ok-N (4.60)
Note that ‘k-N and ok-N are functions of the expansion point x-. To obtain the standard deviation in the equivalent normal space, one can take the derivative on both sides of Eq. (4.59) with respect to xk, resulting in
![]() fk(xk-) = – Xф (xLz»2L
fk(xk-) = – Xф (xLz»2L
in which fk ( ) and ф ( ) are the marginal PDFs of the stochastic basic variable Xk and the standard normal variable Zk, respectively. From this equation, the normal equivalent standard deviation ok-N can be computed as
Therefore, according to Eqs. (4.60) and (4.61), the mean and standard deviation of the normal equivalent of the stochastic basic variable Xk can be calculated.
It should be noted that the normal transformation uses only the marginal distributions of the stochastic basic variables without regarding their correlations. Therefore, it is, in theory, suitable for problems involving independent
|
|
|||
|
||||
|
||||
|
||||
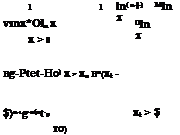 |
||||
|
||||
|
||||
|
||||
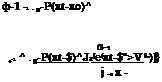 |
||||
|
|
|||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
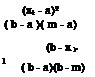 |
||||
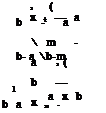 |
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
|
|||
|
||||
|
||||
|
||||
|
||||
nonnormal random variables. When stochastic basic variables are nonnormal but correlated, additional considerations must be given in the normal transformation (see Sec. 4.5.7).
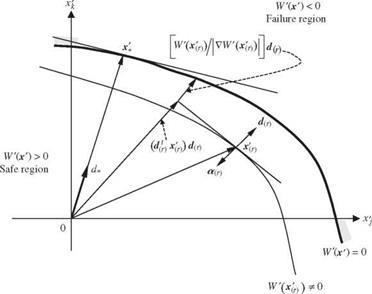
To incorporate the normal transformation for nonnormal uncorrelated stochastic basic variables, the Hasofer-Lind AFOSM algorithm for problems having uncorrelated nonnormal stochastic variables involves the following steps:
Step 1: Select an initial trial solution x(r).
Step 2: Compute the mean and standard deviation of the normal equivalent
using Eqs. (4.60) and (4.61) for those nonnormal stochastic basic variables.
For normal stochastic basic variables, pkN,(r) = дk and akN,(r) = ak.
Step 3: Compute W(x(r>) and the corresponding sensitivity coefficient vector
sx,(r) •
Step 4: Revise solution point x(r+i> according to Eq. (4.52) with the mean
and standard deviations of nonnormal stochastic basic variables replaced by
their normal equivalents, that is,
Step 5: Check if x(r) and x(r+1) are sufficiently close. If yes, compute the reliability index ^AFOSM according to Eq. (4.47) and the corresponding reliability ps = Ф)^^); then, go to step 5. Otherwise, update the solution point by letting x(r) = x(r+1) and return to step 2.
Step 6: Compute the sensitivity of the reliability index and reliability with respect to changes in stochastic basic variables according to Eqs. (4.48), (4.49), and (4.50) with Dx replaced by DxN at the design point x*.
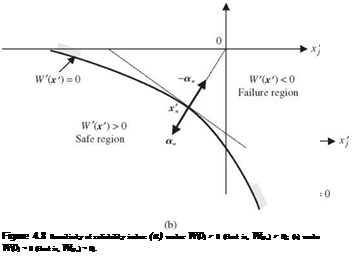
As for the Ang-Tang AFOSM algorithm, the iterative algorithms described previously can be modified as follows (also see Fig. 4.10):
Step 1: Select an initial point x(r) in the parameter space.
Step 2: Compute the mean and standard deviation of the normal equivalent using Eqs. (4.60) and (4.61) for those nonnormal stochastic basic variables. For normal stochastic basic variables, pkN,(r) = Pk and akN,(r) = &k.
Step 3: At the selected point x(r), compute the mean and variance of the performance function W(x(r>) according to Eqs. (4.56) and (4.44), respectively.
Step 4: Compute the corresponding reliability index в(г) according to Eq. (4.8).
Step 5: Compute the values of the normal equivalent directional derivative akN,(r), for all k = 1,2, •••, K, according to Eq. (4.46), in that the standard
deviations of nonnormal stochastic basic variables ak’s are replaced by the corresponding OkN,(r)’s.
Step 6: Using во) and akN,(r) obtained from steps 3 and 5, revise the location of expansion point xо+1) according to
![]() Xk,(r + 1) = PkN,(r) – akN,(r)во)akN,(r) k = 1, 2, … , K
Xk,(r + 1) = PkN,(r) – akN,(r)во)akN,(r) k = 1, 2, … , K
Step 7: Check if the revised expansion point x(r+p differs significantly from the previous trial expansion point x(r). If yes, use the revised expansion point as the new trial point by letting xо) = xо+p, and go to step 2 for another iteration. Otherwise, the iteration is considered complete, and the latest reliability index во) is used to compute the reliability ps = Ф(во)).
Step 8: Compute the sensitivity of the reliability index and reliability with respect to changes in stochastic basic variables according to Eqs. (4.47), (4.48), and (4.49) with D x replaced by DxN at the design point x*.
Example 4.10 (Independent, nonnormal) Refer to the data in Example 4.9 for the
storm sewer reliability analysis problem. Assume that all three stochastic basic variables are independent random variables having different distributions. Manning’s roughness n has a normal distribution; pipe diameter D, lognormal; and pipe slope S, Gumbel distribution. Compute the reliability that the sewer can convey an inflow discharge of 35 ft3/s by the Hasofer-Lind algorithm.
Solution The initial solution is taken to be the means of the three stochastic basic variables, namely, xq) = p, x = (pn, xd, xs) = (0.015, 3.0, 0.005)г. Since the stochastic basic variables are not all normally distributed, the Rackwitz normal transformation is applied. For Manning’s roughness, no transformation is required because it is a normal stochastic basic variable. Therefore, fin, N,(1) = Xn = 0.015 and an, n,(i) = an = 0.00075.
For pipe diameter, which is a lognormal random variable, the variance and the mean of log-transformed pipe diameter can be computed, according to Eqs. (2.67a) and (2.67b), as
![]()
= ln( 1 + 0.022) = 0.0003999
The standard normal variate zd corresponding to D = 3.0 ft. is
zd = [ln( 3) — xln D iMn D = 0.009999
Then, according to Eqs. (4.60) and (4.61), the standard deviation and the mean of normal equivalent at D = 3.0 ft. are, respectively,
Xd, N,(1) = 2.999 ад, n,(1) = 0.05999
For pipe slope, the two parameters in the Gumbel distribution, according to Eqs. (2.86a) and (2.86b), can be computed as
в = ,°S = 0.0001949
V1.645
§ = дS — 0.577в = 0.004888
The value of reduced variate Y = (S — §)/в at S = 0.005 is Y = 0.577, and the corresponding value of CDF by Eq. (2.85a) is Fev1(Y = 0.577) = 0.5703. According to Eq. (4.59), the standard normal quantile corresponding to the CDF of 0.5703 is Z = 0.1772. Based on the available information, the values of PDFs for the standard normal and Gumbel variables, at S = 0.005, can be computed as ф(Z = 0.1722) = 0.3927 and /"ev/Y = 0.577) = 1643. Then, by Eqs. (4.61) and (4.60), the normal equivalent standard deviation and the mean for the pipe slope, at S = 0.005, are
Hs n (1) = 0.004958 &s n (1) = 0.000239
At x(1) = (0.015, 3.0, 0.005/, the normal equivalent mean vector for the three stochastic basic variables is
VN ,(1) = (Дп, N ДЬ VD, N ДЬ д-S, N,(1)/ = (°.°15, 2.999, °.°04958)< and the covariance matrix is
|
2 an, N |
0 |
0 |
0.000752 |
0 |
0 |
||
|
D N,(1) = |
1 О О |
2 aD, N 0 |
0 2 aS, N. |
= |
1 О О |
0.05992 0 |
0 0.0002392 _ |
At x(1), the sensitivity vector sx,(1) is
sX;(1) = (9W/дn, dW/дD, dW/дS) = (—2734, 36.50, 4101/
and the value of the performance function W(n, D, S) = 6.010, is not equal to zero. This implies that the solution point x(1) does not lie on the limit-state surface. Applying Eq. (4.62) using normal equivalent means vn and variances Dxn and the new solution x(2) can be obtained as x(2) = (0.01590, 2.923, 0.004821/. Then one checks the difference between the two consecutive solutions as
9 = | x(1) — x(2)| = [(0.0159 — 0.015)2 + (2.923 — 3.0)2 + (0.004821 — 0.005)2]a5 = 0.07729
which is considered large, and therefore, the iteration continues. The following table lists the solution point x(r), its corresponding sensitivity vector sx,(r), and the vector of directional derivatives aN,(r) in each iteration. The iteration stops when the difference between the two consecutive solutions is less than 0.001 and the value of the performance function is less than 0.001.
|
Iteration |
Var. |
x(r) |
,(r) |
&N,(r) |
sx,(r) |
aN,(r) |
x (r +1) |
|||
|
r |
= 1 |
n |
0.1500 x |
10—01 |
0.1500 x 10—01 |
0.7500 x 10—03 |
—0.2734 x 10+04 |
—0.6497 x 10+00 |
0.1590 |
x 10—01 |
|
D |
0.3000 x |
10+01 |
0.2999 x 10+01 |
0.5999 x 10—01 |
0.3650 x 10+02 |
0.6938 x 10+00 |
0.2923 |
x 10+01 |
||
|
S |
о Ql о о о X |
10—02 |
0.4958 x 10—02 |
0.2390 x 10—03 |
0.4101 x 10+04 |
0.3106 x 10+00 |
0.4821 |
x 10—02 |
||
|
5 |
= 0.7857 x 10—01 |
W = 0.6010 x 10+01 |
в = 0.0000 x 10+00 |
|||||||
|
r |
= 2 |
n |
0.1590 x |
10—01 |
0.1500 x 10—01 |
0.7500 x 10—03 |
—0.2229e+04 |
—0.6410e+°° |
0.1598 |
x 10—01 |
|
D |
0.2923 x |
10+01 |
0.2998 x 10+01 |
0.5845 x 10—01 |
0.3237 x 10+02 |
0.7255 x 10+00 |
0.2912 |
x 10+01 |
||
|
S |
0.4821 x |
10—02 |
0.4944 x 10—02 |
0.1778 x 10—03 |
0.3675 x 10+04 |
0.2505 x 10+00 |
0.4853 |
x 10—02 |
||
|
5 |
= 0.1113 x 10—01 |
W = 0.4371 x 10+00 |
в = 0.1894 x 10+01 |
|||||||
|
r |
= 3 |
n |
0.1598 x |
10—01 |
0.1500 x 10—01 |
0.7500 x 10—03 |
—0.2190 x 10+04 |
—0.6369 x 10+00 |
0.1598 |
x 10—01 |
|
D |
0.2912e+01 |
0.2998e+01 |
0.5823 x 10—01 |
0.3210 x 10+02 |
0.7247 x 10+00 |
0.2912 |
x 10+01 |
|||
|
S |
0.4853 x |
10—02 |
0.4950 x 10—02 |
0.1880 x 10—03 |
0.3607 x 10+04 |
0.2630e+00 |
0.4849 |
x 10—02 |
||
|
5 |
= 0.1942 x 10—04 |
W = 0.2147 x 10—02 |
в = 0.2049 x 10+01 |
|||||||
|
r |
= 4 |
n |
0.1598 x |
10—01 |
0.1500 x 10—01 |
0.7500 x 10—03 |
—0.2190 x 10+04 |
—0.6373 x 10+01 |
0.1598 |
x 10—01 |
|
D |
0.2912 x |
10+01 |
0.2998 x 10+01 |
0.5823 x 10—01 |
0.3210 x 10+02 |
0.7249 x 10+00 |
0.2912 |
x 10+01 |
||
|
S |
0.4849 x |
10—02 |
0.4949 x 10—02 |
0.1867 x 10—03 |
0.3609 x 10+04 |
0.2614 x 10+00 |
0.4849 |
x 10—02 |
||
|
5 |
= 0.2553 x 10—04 |
W = 0.3894 x 10—05 |
в = 0.2050 x 10+01 |
After four iterations, the solution converges to the design point x* = (n*, D*, S*)г = (0.01598, 2.912, 0.004849)г. At the design point x*, the mean and standard deviation of the performance function W can be estimated by Eqs. (4.42) and (4.43), respectively, as
Hw* = 5.285 and aw* = 2.578
The reliability index then can be computed as в* = iw l°w* = 2.050, and the corresponding reliability and failure probability can be computed, respectively, as
ps = Ф(в*) = 0.9798 pf = 1 — ps = 0.02019
Finally, at the design point x*, the sensitive of the reliability index and reliability with respect to each of the three stochastic basic variables can be computed by Eqs. (4.49) and (4.50). The results are shown in columns (4) to (7) in the following table:
|
Variable (1) |
x (2) |
aN,* (3) |
дв/д z (4) |
д ps |д z (5) |
дв/д x (6) |
дps/д x (7) |
хдв/вдx (8) |
xд psl psд x (9) |
|
n |
0.01594 |
—0.6372 |
0.6372 |
0.03110 |
849.60 |
41.46 |
6.623 |
0.6762 |
|
D |
2.912 |
0.7249 |
—0.7249 |
—0.03538 |
—12.45 |
—0.61 |
—17.680 |
—1.8060 |
|
S |
0.00483 |
0.2617 |
—0.2617 |
—0.01277 |
—1400.00 |
— 68.32 |
—3.312 |
—0.3381 |
The sensitivity analysis yields a similar indication about the relative importance of the stochastic basic variables, as in Example 4.9.