Bounds for system reliability
Despite the system under consideration being a series or parallel system, the evaluation of system reliability or failure probability involves probabilities of union or intersection of multiple events. Without losing generality, the derivation of the bounds for P (A1U A2 U—U AM) and P (A1 n A2 П—П AM) are given below.
For example, consider P(A1 U A2 U-U AM). When Am = Fm, the probability is for the failure probability of a series system, whereas when Am = Fm, the probability is for the reliability of a parallel system. The bounds of system failure probability, that is, can be defined as follows:
Pf ,sys – Pf, sys – Pf, sys (7.11a)
with p f sys and p f, sys being the lower and upper bounds of system failure probability, respectively. The corresponding bounds for system reliability can be obtained as
1 – Pf, sys = PS, SyS – Ps, sys – Ps, sys = 1 – Pf, sys (7.11b)
Similarly, after the bounds on system reliability are obtained, the bounds on system failure reliability can be computed easily.
First-order bounds. These bounds also are called unimodal bounds (Ang and Tang, 1984, p. 450). They can be derived as follows. Referring to Eq. (2.7), the probability of the joint occurrence of several events can be computed as
P ( П A^ = P (A1) x P (A2 | A1) x—x P ( Am | Am-1, Am-2, ■ ■■, A2, A1)
m=1 )
(7.12)
Under the condition that all events Aj and Am are positively correlated, the following inequality relationship holds:
P (Am | Aj ) > P (Am)
Hence
P (Aj, Am) = P (Am | Aj)P ( Aj ) > P ( Am)P (Aj )
This can be extended to a multiple-event case as
|
|||
|
|
||
|
|||

As can be seen, the lower bound of the probability of an intersection is when all events are as if they are independent. Furthermore, it is also true that
П Am c Aj for any j = 1, 2, ■■■, M
m=1
Therefore,
![]() c min{ A1, A2, ■■■, Am }
c min{ A1, A2, ■■■, Am }
Consequently,
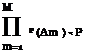 |
|||
Based on Eqs. (7.13) and (7.14), the bounds on probability of joint occurrence of several positively correlated events are
Example 7.3 Consider three standardized normal random variables Z1, Z2, and Z3 with the following correlation matrix:
|
1.000 |
0.841 |
0.014 |
|
|
Rz = |
0.841 |
1.000 |
0.536 |
|
0.014 |
0.536 |
1.000 |
Compute the first-order bounds for P{(Z1 < —2.71) U (Z2 < —2.88) U (Z3 < —3.44)}.
Solution The three events corresponding to the preceding trivariate normal probability are
A1 = {Z1 < -2.71} A2 = {Z2 < -2.88} A3 = {Z3 < -3.44}
Since,
P(A1 U A2 U A3) = 1 — P(Aj П A П A3)
the first-order bounds for P( A1U A2 U A3) can be obtained from those of P(A1П A П A3).
To derive the first-order bounds for P(A1 П A П A3), individual probabilities are required, which can be obtained from Table 2.2 or Eq. (2.63) as
P(A[) = P(Z1 > -2.71) = 0.99664
P(A2) = P(Z2 > -2.88) = 0.99801
P(A3) = P(Z3 > -3.44) = 0.99971
Furthermore, because all Am’s are positively correlated, all Am’s are also positively correlated. According to Eq. (7.15), the first-order bounds for P(A1 П A^ П A3) is
(0.99664)(0.99801)(0.99971) < P[ n Am) < min{0.99664, 0.99801, 0.99971}
m=1
which can be reduced to
Therefore, the corresponding first-order bounds for P(A1 U A2 U A3) is
which can be reduced to
Referring to Eq. (7.2), the first-order bounds for reliability of a series system with positively correlated nonfailure events can be computed as
M
П P (Fm) < ps, SyS < min{P (Fm)} (7.16a)
m=1
or in terms of failure probability as
M
IT [1 – P (Fm)] < Ps, sys < min{1 – P (Fm)} (7.16b)
m
m=1
Similarly, referring to Eq. (7.7), by letting Am = Fm, the first-order bounds on the failure probability of a parallel system with positively correlated failure events can be immediately obtained as
M
TT P(Fm) < Pf, sys < min{P(Fm)} (7.17a)
m
m=1
and the corresponding bounds for the system reliability, according to Eq. (7.11b), is
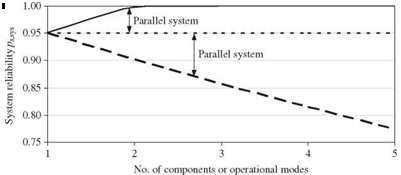
Example 7.4 Consider that the M identical components in a system are positively correlated and the component reliability is ps. Determine the reliability bounds for the system.
Solution If the system is a series system, the bounds on system reliability, according to Eq. (7.16a), are
PM < Ps, sys < Ps
When the system is in parallel, the bounds on the system reliability, according to Eq. (7.17b), are
Ps < Ps, sys < 1 – (1 – Ps)M
The bounds for system reliabilities for different M, with the component reliability of 0.95, for series and parallel systems are shown in Fig. 7.6. As can be observed, the bounds for the system widen as the number of components increases.
In the case that all events Am’s are negatively correlated, the following relationships hold:
P (Am | Aj) < P (Aj) for all j, m
P(Aj, Am) < P(Aj )P(Am)
Hence the first-order bounds for the probability of joint occurrence of several negatively correlated events is
![]()
![]()
 |
M
< П P (Am)
m=1
The bounds for reliability of a series system, with Am = F’m, containing negatively correlated events are
M
0 < Ps, sys < [1 – P (Fm)]
m=1
![]()
whereas for a parallel system, with Am = Fm,
It should be pointed out that the first-order bounds for system reliability may be too wide to be meaningful. Tighter bounds sometimes are required and can be obtained at the expense of more computations.
Second-order bounds (Bimodal bounds). The second-order bounds are obtained by retaining the terms involving the joint probability of two events. By Eq. (2.4), the probability of the union of several events is
p(u Am) = E P (Am)-EE P (Ai, Aj) + Y, P (Ai, Aj, Ak)-•••
‘ ‘ m=1 i< j i< j < k
+ (-1) MP (A1, A2,…, Am ) (7.18)
Notice the alternating signs in Eq. (7.18) as the order of the terms increases. It is evident that the inclusion of only the first-order terms, that is, P(Am), produces an upper bound for P (A1 U A2 U ■ ■ ■ U AM). Consideration of the only the first two order terms yields a lower bound, the first three order terms again an upper bound, and so on (Melchers, 1999).
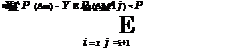 |
|||
Simple bounds for the probability of a union are
It should be pointed out that these bounds produce adequate results only when the values of P(Am) and P(Am, Aj) are small. Equation (7.18) alternatively can be written as
P M Am) = [P (A1)] + [P (A2) – P (A1, A2)] + [ P (A3) – P (A1, A3)
m=1
— P (A2, A3) + P (A1, A2, A3)] + [P (A4) — P (A1, A4) — P (A2, A4)
— P (A3, A4) + P (A1, A2, A4) + P (A1, A3, A4) + P (A2, A3, A4)
— P (A1, A2, A3, A4)] + [P (A5) ••• (7.20)
To derive the lower bound, consider each of the terms in brackets in Eq. (7.20). For example, consider the bracket containing the terms associated with event A4. Note that apart from P(A4), the remaining terms in the bracket are
-P [(A1, A4) U (A2, A4) U (A3, A4)]
Furthermore, event A4 contains (A1, A4)U(A2, A4)U(A3, A4), which implies that P (A4) > P [(A1, A4) U (A2, A4) U (A3, A4)]. Consequently, each of the bracketed terms in Eq. (7.20) has a nonnegative probability value. Also notice that
and thus the following inequality holds:
![]()
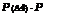 3
3
> P(A4) – Y P (Aj, At)
j=1
This equation can be generalized as
![]() m-1
m-1
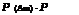 > P(Am) – Y P (Aj, Am) (7.21)
> P(Am) – Y P (Aj, Am) (7.21)
j=1
It should be pointed out that the terms on the right-hand-side of Eq. (7.21) could be negative, especially when m is large. Owing to the fact that each of the
bracketed terms should be nonnegative, abetter lower bound to Eq. (7.20) can be obtained if the right-hand-side of Eq. (7.21) makes a nonnegative contribution to the lower bound (Ditlevsen, 1979), namely,
Earlier, Kounias (1968) proposed an alternative second-order lower bound by selecting only those combinations in Eq. (7.20) which give the maximum values of the lower bound:
pQ^ Am^j > P(A1) + max J ^[P(Am) – P(Aj, Am)](7.23)
j <m J
It should be pointed out that both lower bounds for the probability of a union depend on the order in which the events are labeled. Algorithms have been developed for identifying the optimal ordering of events to obtain the best bounds (Dawson and Sankoff, 1967; Hunter, 1977). A useful rule of thumb is to order the events in the order of decreasing importance (Melchers, 1999). In other words, events are ordered such that P(A[1]) > P ( A[2]) > ••• > P(A[M]), with [m] representing the rank of the event according to its probability of occurrence. For a given ordering, Ramachandran (1984) showed that the lower bound provided by Eq. (7.22) is better than Eq. (7.23), whereas both bounds are equal if all possible orderings are considered.
To derive the upper bound, attention is focused back to Eq. (7.20) and on each of the terms in brackets. For example, consider the bracket containing the terms associated with event A4. As discussed earlier, apart from P ( A4), the remaining terms in the bracket are
—P [(A1, A4) U (A2, A4) U (A3, A4)]
Using the fact that P(A U B) > max[P(A), P(B)], the following inequality holds:
![]() U (Aj, A4) > max[P(Aj, A4)]
U (Aj, A4) > max[P(Aj, A4)]
Lj <4 j j <4
Hence the probability in the fourth bracket involving event A4 satisfies
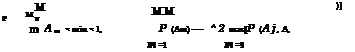 |
|
This inequality relation is true for all the bracketed terms of Eq. (7.22), and the upper bound can be obtained as
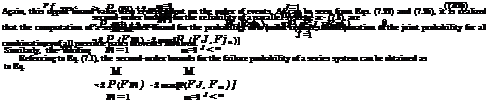
Example 7.5 Refer to Example 7.3. Compute the second-order bounds for the multivariate normal probability.
Solution To compute the second-order bounds, the probabilities of individual events as well as the joint probabilities between two different event pairs must be computed. From Table 2.2 or Eq. (2.63), the probabilities of individual events are
P(A1) = P(Z1 < -2.71) = 0.003364
P(A2) = P(Z2 < -2.88) = 0.001988
P(A3) = P(Z3 < -3.44) = 0.0002909
The joint probabilities, according to the procedures described in Sec. 2.7.2, are P(A1, A2) = P(Z1 < -2.71, Z2 < -2.88 | p = 0.841) = 0.0009247
P(A1, A3) = P(Z1 < -2.71, Z3 < -3.44 | p = 0.014) = 0.000001142
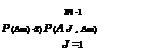 |
||
P(A2, A3) = P(Z2 < -2.88, Z3 < -3.44 | p = 0.536) = 0.00004231 The lower bound of P(A1 U A2 U A3), according to Eq. (7.23), is
= P(A1) + max{[P(A2) – P(A1, A2)], ^ + max{[P(A3) – P(A1, A2) – P(A2, Ae)],0} = 0.003364 + max[[0.001988 – 0.0009247], 0} +max{[2.909 x 10-4 – 1.142 x 10-6) -4.231 x 10-5], 0} = 0.003364 + 0.00106633 + 0.00024736 = 0.004675
The upper bound of P(Ai U A2 U A3), according to Eq. (7.25), can be computed as
3 3
V P(Am) – У max[P(Aj, Am)]
m=1 m=2
3
= У P(Am) – {max[P(A1, A2)] + max[P(A1, A3), P(A2, A3)]}
m=i
= (0.003364 + 0.001988 + 0.002909) У max(0.0009247)
+ max[(1.142 x 10-6, 4.231 x 10-5)]} = 0.005641 – (0.000924 + 0.0000425)
= 0.004677
In summary, the second-order bounds for the trivariate normal probability P (A1 U A2 U A3) are
0.004675 < P(A1 U A2 U A3) < 0.004677
Comparing with the first-order bounds obtained in Example 7.3, the second-order bounds are definitely tighter.






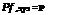 mUi Fm) = £ P(Fm) _^ X) P(Fi, F,)
mUi Fm) = £ P(Fm) _^ X) P(Fi, F,)






 G = -]T (g(i) – Z* g/(i)) + Z* e (g о
G = -]T (g(i) – Z* g/(i)) + Z* e (g о
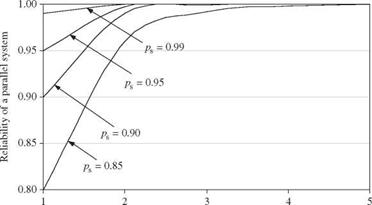
 monotonic in each of the Xk, the variances of the estimators are no more than and often less than the variances when random variables are generated from simple random sampling. McKay (1988) suggested that the use of twice the number of involved random variables for sample size (M > 2K) would be sufficient to yield accurate estimation of the statistics model output. Iman and Helton (1985) indicated that a choice of M equal to 4/3K usually gives satisfactory results. For a dynamic stream water-quality model over a 1-year simulation period, Manache (2001) compared results from LHS using M = 4/3K and M = 3K and found reasonable convergence in the identification of the most sensitive parameters but not in calculation of the standard deviation of model output. Thus, if it is computationally feasible, the generation of a larger number of samples would further enhance the accuracy of the estimation. Like all other variance-reduction Monte Carlo techniques, LHS generally would require fewer samples or model evaluations to achieve an accuracy level comparable with that obtained from a simple random sampling scheme. In hydrosystems engineering, the LHS technique has been applied widely to sediment transport (Yeh and Tung, 1993; Chang et al., 1993), water-quality modeling (Jaffe and Ferrara, 1984; Melching and Bauwens, 2001; Sohrabi et al., 2003; Manache and Melching, 2004), and rainfall-runoff modeling (Melching, 1995; Yu et al., 2001; Christiaens and Feyen, 2002; Lu and Tung, 2003).
monotonic in each of the Xk, the variances of the estimators are no more than and often less than the variances when random variables are generated from simple random sampling. McKay (1988) suggested that the use of twice the number of involved random variables for sample size (M > 2K) would be sufficient to yield accurate estimation of the statistics model output. Iman and Helton (1985) indicated that a choice of M equal to 4/3K usually gives satisfactory results. For a dynamic stream water-quality model over a 1-year simulation period, Manache (2001) compared results from LHS using M = 4/3K and M = 3K and found reasonable convergence in the identification of the most sensitive parameters but not in calculation of the standard deviation of model output. Thus, if it is computationally feasible, the generation of a larger number of samples would further enhance the accuracy of the estimation. Like all other variance-reduction Monte Carlo techniques, LHS generally would require fewer samples or model evaluations to achieve an accuracy level comparable with that obtained from a simple random sampling scheme. In hydrosystems engineering, the LHS technique has been applied widely to sediment transport (Yeh and Tung, 1993; Chang et al., 1993), water-quality modeling (Jaffe and Ferrara, 1984; Melching and Bauwens, 2001; Sohrabi et al., 2003; Manache and Melching, 2004), and rainfall-runoff modeling (Melching, 1995; Yu et al., 2001; Christiaens and Feyen, 2002; Lu and Tung, 2003).



 pm&m
pm&m
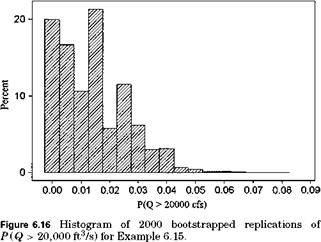
![Correlated-sampling techniques Подпись: Example 6.12 Refer to the pump reliability problem that has been studied in previous examples. Now consider a second pump the time-to-failure PDF of which also is an exponential distribution but has a different parameter of в = 0.0005/h. Estimate the difference in the failure probability between the two pumps over the time interval [0, 200 h] using the correlated-sampling technique with n = 2000. Solution Again, the sample-mean Monte Carlo method with a uniform distribution U(0, 200) is applied as in Example 6.7. In this example, the same set of standard uniform random variates {u1, U2,..., U2000} fromU(0,1) is used to estimate the failure probabilities for the two pumps as](/img/1312/image959_1.png)