Correlated-sampling techniques are especially effective for variance reduction when the primary objective of the simulation study is to evaluate small changes in system performance or to compare the difference in system performances between two specific designs (Rubinstein, 1981; Ang and Tang, 1984). Consider that one wishes to estimate
A© = ©1 — ©2
in which
©1 = J g1(x) f 1(x) dx = E [ g1(X)] ©2 = / g2(y) f2(y) dy = E [ g2(Y)]
 |
 |
 |
 |
 |
with f 1(x) and f 2(y) being two different PDFs. By Monte Carlo simulation, A© can be estimated as
in which Xi andYi are random samples generated from f 1(x) and f2(y), respectively, and A©i = g1(Xi) — gjjYi).
The variance associated with A© is
Var(A©) = Var(©©1) + Var(©2) — 2Cov(©b ©2) (6.83)
In the case that random variates Xi and Yi are generated independently in the Monte Carloalgorithm, ©1 and ©2 also would be independent random variables.
Hence Var(A©) = Var((©1) + Var(©2)________________________
Note that from Eq. (6.83), Var(A©) can be reduced if positively correlated random variables ©1 and ©2 can be produced to estimate A©. One easy way to obtain positively correlated samples is to use the same sequence of uniform random variates from U(0, 1) in both simulations. That is, the random sequences {X1, X 2,…, Xn} and {Y1, Y 2,…, Yn} are generated through Xi = F—l(Ui) and Yi = F—1(Ui), respectively.
The correlated-sampling techniques are especially effective in reducing variance when the performance difference between two specific designs for a system involve the same or similar random variables. For example, consider two designs A and B for the same system involving a vector of K random variables X = (X1, X2,…, XK), which could be correlated with a joint PDF fx(x) or be independent of each other with a marginal PDF fk(xk), k = 1, 2,…, K. The performance of the system under the two designs can be expressed as
 |
 |
 |
 |
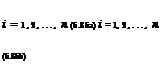![Подпись: Example 6.12 Refer to the pump reliability problem that has been studied in previous examples. Now consider a second pump the time-to-failure PDF of which also is an exponential distribution but has a different parameter of в = 0.0005/h. Estimate the difference in the failure probability between the two pumps over the time interval [0, 200 h] using the correlated-sampling technique with n = 2000. Solution Again, the sample-mean Monte Carlo method with a uniform distribution U(0, 200) is applied as in Example 6.7. In this example, the same set of standard uniform random variates {u1, U2,..., U2000} fromU(0,1) is used to estimate the failure probabilities for the two pumps as](/img/1312/image959_1.png "Correlated-sampling techniques") |
 |
 |
 |
 |
![Подпись: which is within 0.125 percent of the exact solution e 0 0005(20°) — e о.оооазоо) = e-01 — e—016 = 0.0526936. The standard deviation of the 2000 differences in failure probability Ai = 200[ fA(ti) — fB (ti)], i = 1,2,... ,2000, is 0.00405. Hence the standard error associated with the estimated difference in failure probability is 0.00405/V2000 = 0.00009.](/img/1312/image964_0.png "Correlated-sampling techniques"){kind=small} |
in which g( ) is a function defining the system performance, and a and b are vectors of design parameters corresponding to designs A and B, respectively. Since the two performance measures ©A and ©B are dependent on the same random variables through the same performance function g( ), their estimators will be positively correlated. In this case, independently generating two sets of K random variates, according to their probability laws for designs A and B, still wouldresult in a positive correlation between ©A and ©B. To further reduce Var(A©), an increase in correlation between ©A and ©B can be achieved using a common set of standard uniform random variates for both designs A and B by assuming that system random variables are independent, that is,
For the sake of examining the effectiveness of the correlated-sampling technique, let us separately generate a set of independent standard uniform random variates {Ир u2,…, U2000} and use them in calculating the failure probability for pump B. Then the estimated difference in failure probability between the two pumps is 0.05256, which is slightly larger than that obtained by the correlated-sampling technique. However, the standard error associated with Ai = 200[f a(4) — f в(t)] then is
0. 00016, which is larger than that from the correlated-sampling technique.
