A tool such as that shown in Fig. 7.57 can be constructed out of pipe to straighten twisted U-channel posts [48]. Similar devices with a metal U-shape at the end of a pipe handle can be constructed to realign shaped wood posts and square tubing. A large pipe wrench can also be used to realign U-channel and square-tube supports. Small signs should be mounted at 90° to the road.
U. S. Customary Units, in
|
A.
|
1 Pc – 38 I. D. BLACK PIPE – 1270 LONG
|
1.5 I. D.—48
|
|
B.
|
1 Pc – 16 X 75 X 255 LONG
|
s/e X 3 X 10
|
|
c.
|
1 Pc-20 X 20 X 15 LONG
|
3/4 X 3/4 X V2
|
|
D.
|
1 Pc-6 x 20 x 510 LONG
|
1/4 X 3/4 X 20
|
|
E.
|
1 Pc – 10 X 10 X 75 LONG
|
3/8 X 3/B X 3
|
|
R
|
1 – CLEVIS SLIP HOOK (REMOVE EYE)
|
|
|
FIGURE 7.57 Shop-fabricated tool to straighten twisted U-channel.
|
7.9 REFERENCES ON SIGNING
1. Manual on Uniform Traffic Control Devices, American Association of State Highway Officials and National Conference on Street and Highway Safety, Washington, D. C., 1935.
2. Manual on Uniform Traffic Control Devices for Streets and Highways, Federal Highway Administration, U. S. Department of Transportation, Washington, D. C., 2003.
3. Traffic Control Devices Handbook, Federal Highway Administration, U. S. Department of Transportation, Washington, D. C., 1983.
4. Bowman, Brian L., NCHRP Synthesis of Highway Practice 186: Supplemental Advance Warning Devices, Transportation Research Board, National Research Council, Washington, D. C., 1993.
5. Harwood, Douglas W., NCHRP Synthesis of Highway Practice 191: Use of Rumble Strips to Enhance Safety, Transportation Research Board, National Research Council, Washington, D. C., 1993.
6. Cunard, Richard A., NCHRP Synthesis of Highway Practice 157: Maintenance Management of Street and Highway Signs, Transportation Research Board, National Research Council, Washington, D. C., 1990.
7. “1988 Annual Report on Highway Safety Improvement Programs,” Report of the Secretary of Transportation to the United States Congress, Report No. FHWA-SA-88-0003, Federal Highway Administration, U. S. Department of Transportation, Washington, D. C., 1988.
8. Lewis, Russel M., NCHRP Synthesis of Highway Practice 106: Practical Guidelines for Minimizing Tort Liability, Transportation Research Board, National Research Council, Washington, D. C., 1983.
9. Standard Highway Signs, Including Pavement Markings and Standard Alphabets, 2004 Version, U. S. Department of Transportation. Federal Highway Administration, Washington, D. C., 2004.
10. Roadside Design Guide, American Association of State Highway and Transportation Officials, Washington, D. C., 2002.
11. Delphi V—Forecast and Analysis of the U. S. Automotive Industry through the Year 2000, University of Michigan Transportation Research Institute, Ann Arbor, July 1989.
12. Standard Specifications for Structural Supports for Highway Signs, Luminaires and Traffic Signals, American Association of State Highway and Transportation Officials, Washington, D. C., 2001, and Interim Specifications, 2002, 2003, and 2006.
13. Mickie, J. D., “Recommended Procedures for the Safety Performance Evaluation of Highway Appurtenances,” NCHRP Report 230, Transportation Research Board, Washington, D. C., March 1987.
14. Ross, Hayes, Jr., Dean L. Sicking, Richard A. Zimmer, and Jarvis D. Mickie, “Recommended Procedures for the Safety Performance Evaluation of Highway Features,” NCHRP Report 350, Transportation Research Board, National Research Council, Washington, D. C., 1993.
15. Cunard, Richard A., NCHRP Synthesis of Highway Practice 157; Maintenance Management of Street and Highway Signs, Transportation Research Board, National Research Council, Washington, D. C., 1990.
16. Perkins, David, D., “Manual on Countermeasures for Sign Vandalism,” Report No. FHWA – IP-86-7, Federal Highway Administration, Washington, D. C., September 1986.
17. Texas Transportation Institute, “State of the Practice in Supports for Small Highway Signs,” Technology Sharing Report 80-222, Federal Highway Administration, Washington, D. C., 1980.
18. Heinz, Ronald E., “Request for Technical Assistance: Sign Support Design,” Memorandum, Federal Highway Administration, Highway Design Division, Washington, D. C., July 1985.
19. Hayes, E. Ross, Jr., Jesse L. Buffington, et al., “State of the Practice in Supports for Small Highway Signs,” Federal Highway Administration, Washington, D. C., 1980.
20. Composite Technologies Company, Signs Manufactured from 100% Landfill-Destined Plastic, undated brochure, Composite Technologies Company, Dayton, Ohio.
21. Standard Specifications for Highway Signs, Luminaires and Traffic Signals, American Association of State Highway and Transportation Officials, Technical Committee, Washington, D. C., 1985.
22. Phillips, David K., “Steel Flanged Channel Posts for Small Highway Sign Supports,” technical advisory, Federal Highway Administration, Office of Engineering, Washington, D. C., September 27, 1983.
23. Staron, L. A., “Minute Man Breakaway Device,” letter, Federal Highway Administration, Federal Aid and Design Division, Washington, D. C., January 1987.
24. Heinz, Ronald E., “Splicing of U-Channel Steel Posts,” memorandum, Federal Highway Administration, Highway Design Division, Washington, D. C., October 1984.
25. Noel, Leon M., “Timber Sign Supports,” letter, Federal Highway Administration, Highway Design Division, Washington, D. C., August 1982.
26. Hove, R. W., “Ground Mounted Signs: Timber Sign Supports,” memorandum, Federal Highway Administration, U. S. Department of Transportation, Washington, D. C., May 1984.
27. Allied Tube and Conduit, Qwik-Punch and Qwik-Coat Systems, Harvey, Ill., January 1991.
28. Noble, Glen, “Support System Acceptance,” memorandum, Unistrut Corporation, Wayne, Mich., November 1992.
29. Staron, L. A., “Quick-Punch Sign Supports,” letter, Federal Highway Administration, Federal Aid and Design Division, Washington, D. C., October 3, 1986.
30. Xcessories Squared, Soil Stabilizer (brochure), Auburn, Ill., February 23, 1995.
31. Staron, Lawrence A., Geometric and Roadway Acceptance Letter No. SS-25, Federal Highway Administration, Federal Aid and Design Division, Washington, D. C., June 4,
1991.
32. Staron, L. A., Geometric and Roadside Design Letter No. SS-38, Federal Highway Administration, Federal Aid and Design Division, Washington, D. C., November 1993.
33. Dent Bolt, Trinity Industries, Inc., Highway Safety Products, Dallas, Tex.
34. Staron, L. A., ACTION: Breakaway Sign Supports, memorandum, Federal Highway Administration, Federal Aid and Design Division, Washington, D. C., September 1993.
35. Franklin Steel Eze-Erect™ Sign Posts, Franklin Steel, Franklin, Pa., May 1989.
36. The Minute Man™ U-Channel Breakaway Signpost System, Marion Steel Co., Marion, Ohio,
1992.
37. Staron, L. A., “Splicing of Steel U-Channel Posts on Small Sign Supports,” memorandum, Federal Highway Administration, Federal Aid and Design Division, Washington, D. C., September 1991.
38. Unistrut-Telespar™ Sign Support System, Unistrut Corporation, Wayne, Mich., 1986.
39. Allied Square Tube Signposts, Allied Tube and Conduit, Harvey, Ill., February 1992.
40. 14 Ga. Qwik-Punch System, Allied Tube and Conduit, Harvey, Ill., September 1991.
41. Roadside Improvements for Local Roads and Streets, Office of Highway Safety, Federal Highway Administration, Washington, D. C., October 1986.
42. Staron, L. A., Geometric and Roadside Acceptance Letter No. SS-27, Federal Highway Administration, Federal Aid and Design Division, Washington, D. C., May 1992.
43. Staron, L. A., Geometric and Roadside Acceptance Letter No. LS-23, Federal Highway Administration, Federal Aid and Design Division, Washington, D. C., January 1991.
44. Van Ness, Norman, Acceptance Letter to Southwest Pipe Inc., Highway Design Division, Federal Highway Administration, Washington, D. C., July 1986.
45. Hanna, Howard, “Evaluation of the Upper Hinge Mechanism of Multiple Leg Breakaway Sign Supports,” memorandum, Federal Highway Administration, Program Development Division, Washington, D. C., October 1987.
46. “Maintenance of Small Traffic Signs—A Guide for Street and Highway Maintenance Personnel,” Federal Highway Administration, Report No. FHWA-RT-90-002, Washington, D. C., 1991.
47. Nettleson, Tom, Signs Maintenance Guide, Forest Service, U. S. Department of Agriculture, October 1979.
48. McGee, H. W., et al., “Sign Fabrication, Installation and Maintenance,” Federal Highway Administration, Report No. FHWA-SA-91-033, Washington, D. C., May 1992.
49. Horne, Dwight A., “Slip Base Triple Square Supports in Standard Soil,” Letter No. SS68B, U. S. Department of Transportation, Federal Highway Administration, Washington, D. C., 2004.






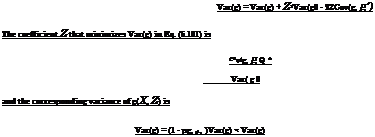
 G = -]T (g(i) – Z* g/(i)) + Z* e (g о
G = -]T (g(i) – Z* g/(i)) + Z* e (g о

