Multivariate lognormal distributions
Similar to the univariate case, bivariate lognormal random variables have a PDF
for x1, x2 > 0, in which
where pln x and ulnx are the mean and standard deviation of log-transformed random variables, subscripts 1 and 2 indicate the random variables X1 and X2, respectively, and p12 = Corr(ln X1, lnX2) is the correlation coefficient of the two log-transformed random variables. After log-transformation is made, properties of multivariate lognormal random variables follow exactly as for the multivariate normal case. The relationship between the correlation coefficients in the original and log-transformed spaces can be derived using the momentgenerating function (Tung and Yen, 2005, Sec. 4.2) as

|
|||
|
|
||
Example 2.23 Resolve Example 2.21 by assuming that both X1 and X2 are bivariate lognormal random variables.
Solution Since X1 and X2 are lognormal variables,
P(X1 < 13, X2 < 3) = P [ln(X1) < ln(13), ln(X2) < ln(3)]
in which »2, a1, and are the means and standard deviations of ln(X1) and ln(X2), respectively; p’ is the correlation coefficient between ln(X1) and ln(X2). The values of »1, »2, a1, and 02 can be computed, according to Eqs. (2.67a) and (2.67b), as
o’x = ] ln(1 + 0.32) = 0.294 e’2 = J ln( 1 + 0.42) = 0.385
p! x = ln(10) – 2(0.294)2 = 2.259 » = ln(5) – 1(0.385)2 = 1.535
Based on Eq. (2.71), the correlation coefficient between ln(X 1) and ln(X2) is
![]() ln[1 + (0.6)(0.3)(0.4)]
ln[1 + (0.6)(0.3)(0.4)]
![]() (0.294)(0.385)
(0.294)(0.385)
Then
P(X1 < 13, X2 < 3 | p = 0.6) = P(Z1 < 1.04, Z2 < -1.13 | p’ = 0.623)
= Ф(а = 1.04, b = -1.13 | p’ = 0.623)
![]()
From this point forward, the procedure for determining Ф(а = 1.04, b = -1.13 | p’ = 0.623) is exactly identical to that of Example 2.21. The result from using Eq. (2.121) is 0.1285.
2.1 Referring to Example 2.4, solve the following problems:
(a) Assume that P(.Ё!!^) = 1.0 and P(E2ІE1) = 0.8. What is the probability that the flow-carrying capacity of the sewer main is exceeded?
(b) If the flow capacity of the downstream sewer main is twice that of its two upstream branches, what is the probability that the flow capacity of the downstream sewer main is exceeded? Assume that if only branch 1 or branch 2 exceeds its corresponding capacity, the probability of flow in the sewer main exceeding its capacity is 0.15.
(c) Under the condition of (b), it is observed that surcharge occurred in the downstream sewer main. Determine the probabilities that (i) only branch 1 exceeds its capacity, (ii) only branch 2 is surcharged, and (iii) none of the sewer branches exceed their capacities.
2.2 Referring to Example 2.5, it is observed that surcharge occurred in the downstream sewer main. Determine the probabilities that (a) only branch 1 exceeds its flow-carrying capacity, (b) only branch 2 is surcharged, and (c) none of the sewer branches exceed their capacities.
2.3 A detention basin is designed to accommodate excessive surface runoff temporarily during storm events. The detention basin should not overflow, if possible, to prevent potential pollution of streams or other receiving water bodies.
For simplicity, the amount of daily rainfall is categorized as heavy, moderate, and light (including none). With the present storage capacity, the detention basin is capable of accommodating runoff generated by two consecutive days of heavy rainfall or three consecutive days of moderate rainfall. The daily rainfall amounts around the detention basin site are not entirely independent. In other words, the amount of rainfall on a given day would affect the rainfall amount on the next day.
Let random variable Xt represent the amount of rainfall in any day t. The transition probability matrix indicating the conditional probability of the rainfall amount in a given day t, conditioned on the rainfall amount of the previous day, is shown in the following table.
|
Xt+1 = |
|||
|
H |
M |
L |
|
|
H |
0.3 |
0.5 |
0.2 |
|
II $ |
0.3 |
0.4 |
0.3 |
|
L |
0.1 |
0.3 |
0.6 |
(a) For a given day, the amount of rainfall is light. What is the probability that the detention basin will overflow in the next three days? (After Mays and Tung, 1992.)
(b) Compute the probability that the detention basin will overflow in the next three days. Assume that at any given day of the month the probabilities for having the various rainfall amounts are P(H) = 0.1, P(M) = 0.3, P (L) = 0.6.
2.4 Before a section of concrete pipe of a special order can be accepted for installation in a culvert project, the thickness of the pipe needs to be inspected by state highway department personnel for specification compliance using ultrasonic reading. For this project, the required thickness of the concrete pipe wall must be at least 3 in. The inspection is done by arbitrarily selecting a point on the pipe surface and measuring the thickness at that point. The pipe is accepted if the thickness from the ultrasonic reading exceeds 3 in; otherwise, the entire section of the pipe is rejected. Suppose, from past experience, that 90 percent of all pipe sections manufactured by the factory were found to be in compliance with specifications. However, the ultrasonic thickness determination is only 80 percent reliable.
(a) What is the probability that a particular pipe section is well manufactured and will be accepted by the highway department?
(b) What is the probability that a pipe section is poorly constructed but will be accepted on the basis of ultrasonic test?
2.5 A quality-control inspector is testing the sample output from a manufacturing process for concrete pipes for a storm sewer project, wherein 95 percent of the items are satisfactory. Three pipes are chosen randomly for inspection. The successive
quality evaluations may be considered as independent. What is the probability that (a) none of the three pipes inspected are satisfactory and (b) exactly two are satisfactory?
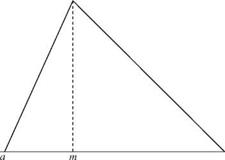
2.6 Derive the PDF for a random variable having a triangular distribution with the lower bound a, mode m, and the upper bound b, as shown in Fig. 2P.1.
2.7 Show that F 1(sq) + F2(x^) – 1 < F^xb x2) < min[F1(x1), F2(x2)]
2.8 The Farlie-Gumbel-Morgenstern bivariate uniform distribution has the following joint CDF (Hutchinson and Lai, 1990):
Fx, y(x, y) — xy [1 + в(1 – x)(1 – y)] for 0 < x, y < 1
with —1 < в < 1. Do the following exercises: (a) derive the joint PDF, (b) obtain the marginal CDF and PDF of X and Y, and (c) derive the conditional PDFs fx(x|y) and fy(y|x).
2.9 Refer to Problem 2.8. Compute (a) P(X < 0.5, Y < 0.5), (b) P(X > 0.5, Y > 0.5), and (c) P(X > 0.5 | Y = 0.5).
2.10 Apply Eq. (2.22) to show that the first four central moments in terms of moments about the origin are
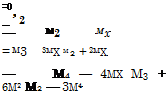 M1 М2 М3 М4
M1 М2 М3 М4
▲
|
|
|
|
2.11 Apply Eq. (2.23) to show that the first four moments about the origin could be expressed in terms of the first four central moments as
m1 = Mx
/ _ ,2 M2 — М2 + Mx
M3 = M3 + 3Mx М2 + m3
M4 = M4 + 4Mx М3 + 6m2 m2 +
2.12 Based on definitions of a – and ^-moments, i. e., Eqs. (2.26a) and (2.26b), (a) derive the general expressions between the two moments, and (b) write out explicitly their relations for r = 0,1, 2, and 3.
2.13 Refer to Example 2.9. Continue to derive the expressions for the third and fourth L-moments of the exponential distribution.
2.14 A company plans to build a production factory by a river. You are hired by the company as a consultant to analyze the flood risk of the factory site. It is known that the magnitude of an annual flood has a lognormal distribution with a mean of 30,000 ft3/s and standard deviation 25,000 ft3/s. It is also known from a field investigation that the stage-discharge relationship for the channel reach is Q = 1500H14, where Q is flow rate (in ft3/s) and H is water surface elevation (in feet) above a given datum. The elevation of a tentative location for the factory is 15 ft above the datum (after Mays and Tung, 1992). (a) What is the annual risk that the factory site will be flooded? (b) At this plant site, it is also known that the flood-damage function can be approximated as
n і – (Нпппч_/0 if H < 15 ft
Damage (in $1000) = |40(lnh + 8)(lnH — 2.7) if H > 15 ft
What is the annual expected flood damage? (Use the appropriate numerical approximation technique for calculations.)
2.15 Referring to Problem 2.6, assume that Manning’s roughness coefficient has a triangular distribution as shown in Fig. 2P.1. (a) Derive the expression for the mean and variance of Manning’s roughness. (b) Show that (i) for a symmetric triangular distribution, a = (b — m)/V6 and (ii) when the mode is at the lower or upper bound, a = (b — a)/3 V2.
2.16 Suppose that a random variable X has a uniform distribution (Fig. 2P.2), with a and b being its lower and upper bounds, respectively. Show that (a) E (X) = xx = (b + a)/2, (b) Var(X) = (b — a)2/12, and (c) ^x = (1 — a/мх)/V3.
2.17 Referring to the uniform distribution as shown in Fig. 2P.2, (a) derive the expression for the first two probability-weighted moments, and (b) derive the expressions for the L-coefficient of variation.
2.18 Refer to Example 2.8. Based on the conditional PDF obtained in part (c), derive the conditional expectation E(Y | x), and the conditional variance Var(Y |x).
Furthermore, plot the conditional expectation and conditional standard deviation of Y on x with respect to x.
2.19 Consider two random variables X and Y having the joint PDF of the following form:
fx, y(X, y) = c (5 – 2 + x2) for 0 < x, y < 2
(a) Determine the coefficient c. (b) Derive the joint CDF. (c) Find fx (x) and fy( y).
(d) Determine the mean and variance of X and Y. (e) Compute the correlation coefficient between X and Y.
2.20 Consider the following hydrologic model in which the runoff Q is related to the rainfall R by
Q = a + bR
if a > 0 and b > 0 are model coefficients. Ignoring uncertainties of model coefficients, show that Corr( Q, R) = 1.0.
2.21 Suppose that the rainfall-runoff model in Problem 2.4.11 has a model error, and it can expressed as
Q = a + bR + є
in which є is the model error term, which has a zero mean and standard deviation of ає. Furthermore, the model error є is independent of the random rainfall R. Derive the expression for Corr( Q, R).
2.22 Let X = X1 + X3 and Y = X2 + X3.FindCorr(X, Y), assuming that X1, X2, and X3 are statistically independent.
2.23 Consider two random variables Y1 and Y2 that each, individually, is a linear function of two other random variables X1 and X2 as follows:
Y1 = anX 1 + a12X 2 Y2 = a21X 1 + a>22X2
It is known that the mean and standard deviations of random variable Xk are and ffk, respectively, for k = 1, 2. (a) Derive the expression for the correlation
coefficient between Y]_ and Y2 under the condition that X1 and X2 are statistically independent. (b) Derive the expression for the correlation coefficient between Y1 and Y2 under the condition that X1 and X2 are correlated with a correlation coefficient p.
2.24 As a generalization to Problem 2.23, consider M random variables Y1, Y2,…, Ym that are linear functions of K other random variables X1, X2,…, Xk in a vector form as follows:
Ym = X for m = 1,2,…, M
in which X = (X1, X2,…, Xk)t, a column vector of K random variables Xs and aim = (am1, am2,…, amK), a row vector of coefficients for the random variable Ym. In matrix form, the preceding system of linear equations can be written as Y = AtX. Given that the mean and standard deviations of the random variable Xk are i^k and Ok, respectively, for k = 1,2,…, K, (a) derive the expression for the correlation matrix between Ys assuming that the random variable Xs are statistically independent, and (b) derive the expression for the correlation coefficient between Y s under the condition that the random variable Xs are correlated with a correlation matrix Rx.
2.25 A coffer dam is to be built for the construction of bridge piers in a river. In an economic analysis of the situation, it is decided to have the dam height designed to withstand floods up to 5000 ft3/s. From flood frequency analysis it is estimated that the annual maximum flood discharge has a Gumbel distribution with the mean of 2500 ft3/s and coefficient of variation of 0.25. (a) Determine the risk of flood water overtopping the coffer dam during a 3-year construction period.
(b) If the risk is considered too high and is to be reduced by half, what should be the design flood magnitude?
2.26 Recompute the probability of Problem 2.25 by using the Poisson distribution.
2.27 There are five identical pumps at a pumping station. The PDFs of the time to failure of each pump are the same with an exponential distribution as Example 2.6, that is,
f (t) = 0.0008 exp(-0.0008t) for t > 0
The operation of each individual pump is assumed to be independent. The system requires at least two pumps to be in operation so as to deliver the required amount of water. Assuming that all five pumps are functioning, determine the reliability of the pump station being able to deliver the required amount of water over a 200-h period.
2.28 Referring to Example 2.14, determine the probability, by both binomial and Poisson distributions, that there would be more than five overtopping events over a period of 100 years. Compare the results with that using the normal approximation.
2.29 From a long experience of observing precipitation at a gauging station, it is found that the probability of a rainy day is 0.30. What is the probability that the next year would have at least 150 rainy days by looking up the normal probability table?
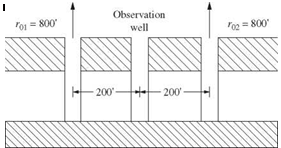
2.30 The well-known Thiem equation can be used to compute the drawdown in a confined and homogeneous aquifer as
in which Sik is drawdown at the ith observation location resulting from a pumpage of Qk at the kth production well, rok is the radius of influence of the kth production well, rik is the distance between the ith observation point and the kth production well, and T is the transmissivity of the aquifer. The overall effect of the aquifer drawdown at the ith observation point, when more than one production well is in operation, can be obtained, by the principle of linear superposition, as the sum of the responses caused by all production wells in the field, that is,
K K
si ‘У ‘sik ‘У ‘hikQk
k = 1 k = 1
where K is the total number of production wells in operation. Consider a system consisting of two production wells and one observation well. The locations of the three wells, the pumping rates of the two production wells, and their zones of influence are shown in Fig. 2P.3. It is assumed that the transmissivity of the aquifer has a lognormal distribution with the mean гт = 4000 gallons per day per foot (gpd/ft) and standard deviation от = 2000 gpd/ft (after Mays and Tung, 1992). (a) Prove that the total drawdown in the aquifer field also is lognormally distributed. (b) Compute the exact values of the mean and variance of the total drawdown at the observation point when Q1 = 10, 000 gpd and Q2 = 15, 000 gpd.
(c) Compute the probability that the resulting drawdown at the observation point does not exceed 2 ft. (d) If the maximum allowable probability of the total drawdown exceeding 2 ft is 0.10, find out the maximum allowable total pumpage from the two production wells.
2.31 A frequently used surface pollutant washoff model is based on a first-order decay function (Sartor and Boyd, 1972):
Mt = M0e-cRt
where M0 is the initial pollutant mass at time t = 0, R is runoff intensity (mm/h), c is the washoff coefficient (mm-1), Mt is the mass of the pollutant remaining
on the street surface (kg), and t is time elapsed (in hours) since the beginning of the storm. This model does not consider pollutant buildup and is generally appropriate for the within-storm event analysis. Suppose that M0 = 10, 000 kg and c = 1.84/cm. The runoff intensity R is a normal random variable with the mean of 10 cm/h and a coefficient of variation of 0.3. Determine the time t such that P(Mt/M0 < 0.05) = 0.90.
2.32 Consider n independent random samples X1, X2,…, Xn from an identical distribution with the mean /xx and variance a2. Show that the sample mean Xn = ^2П= 1 Xi/n has the following properties:
2
E (Xn) = Px and Var( Xn) = ^
n
What would be the sampling distribution of Xn if random samples are normally distributed?
2.33 Consider that measured hydrologic quantity Y and its indicator for accuracy S are related to the unknown true quantity X as Y = SX. Assume that X ~ LN(px, ax), S ~ LN(ps = 1, as), and X is independent of S. (a) What is the distribution function for Y? Derive the expressions for the mean and coefficient of variation of Y, that is, py and Qy, in terms of those of X and S. (b) Derive the expression for rp = yp /xp with P(Y < yp) = P(X < Xp) = p and plot rp versus p. (c) Define measurement error as є = Y — X. Determine the minimum reliability of the measurement so that the corresponding relative absolute error |є/X| does not exceed the require precision of 5 percent.
2.34 Consider that measured discharge Q’ is subject to measurement error є and that both are related to the true but unknown discharge Q as (Cong and Xu, 1987)
Q = Q + є
It is common to assume that (i) E(є | q) = 0, (ii) Var^ | q) = [a(q)q]2, and (iii) random error є is normally distributed, that is, є | q ~ N(рє | q = 0, ає q).
(a) Show that E(Q’ | q) = q, E [(Q’/Q) — 11 q] = 0, and Var[( Q’/Q — 1)2 | q] = a2(q).
(b) Under a(q) = a, showthat E (Q’) = E (Q),VarW = a2 E (Q2),andVar( Q’) = (1 + a2)Var( Q) + a2 E 2( Q). (c) Suppose that it is required that 75 percent of measurements have relative errors in the range of ±5 percent (precision level). Determine the corresponding value of a(q) assuming that the measurement error is normally distributed.
2.35 Show that the valid range of the correlation coefficient obtained in Example 2.20 is correct also for the general case of exponential random variables with parameters в1 and @2 of the form of Eq. (2.79).
2.36 Referring to Example 2.20, derive the range of the correlation coefficient for a bivariate exponential distribution using Farlie’s formula (Eq. 2.107).
2.37 The Pareto distribution is used frequently in economic analysis to describe the randomness of benefit, cost, and income. Consider two correlated Pareto random
variables, each of which has the following marginal PDFs:
adk
fk (xk) = — xk >dk > 0 a > 0, for k = 1,2
xk
Derive the joint PDF and joint CDF by Morgenstern’s formula. Furthermore, derive the expression for E(X1X2) and the correlation coefficient between X1 and X2.
2.38 Repeat Problem 2.37 using Farlie’s formula.
2.39 Analyzing the stream flow data from several flood events, it is found that the flood peak discharge Q and the corresponding volume V have the following relationship:
ln(V) = a + b x ln( Q) + є
in which a and b are constants, and є is the model error term. Suppose that the model error term є has a normal distribution with mean 0 and standard deviation ає. Then show that the conditional PDF of V | Q, h(v |q), is a lognormal distribution. Furthermore, suppose that the peak discharge is a lognormal random variable. Show that the joint PDF of V and Q is bivariate lognormal.
2.40 Analyzing the stream flow data from 105 flood events at different locations in Wyoming, Wahl and Rankl (1993) found that the flood peak discharge Q (in ft3/s) and the corresponding volume V (in acre-feet, AF) have the following relationship:
ln(V) = ln(0.0655) + 1.011 x ln( Q) + є
in which є is the model error term with the assumed ає = 0.3. A flood frequency analysis of the North Platte River near Walden, Colorado, indicated that the annual maximum flood has a lognormal distribution with mean xq = 1380 ft3/s and ffQ = 440 ft3/s. (a) Derive the joint PDF of V and Q for the annual maximum flood. (b) Determine the correlation coefficient between V and Q. (c) Compute P(Q > 2000 ft3/s, V > 180 AF).
2.41 Let X2 = <0) + a1 Z1 + 02 Z2 and X2 = b0 + b1 Z2 + b2 Z^ in which Z1 and Z2 are
bivariate standard normal random variables with a correlation coefficient p, that is, Corr(Z1, Z2) = p. Derive the expression for Corr(X1, X2) in terms ofpolynomial coefficients and p.
2.42 Let X1 and X2 be bivariate lognormal random variables. Show that
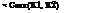
exp ( tfln X1 tfln X2) 1
exp aln x1 aln x2 – 1
What does this inequality indicate?
2.43 Derive Eq. (2.71) from Eq. (2.135):
![]() Corr(lnXi, lnX2) = pi2
Corr(lnXi, lnX2) = pi2
where pi2 = Corr(Xi, X2) and ^ = coefficient of variation of Xk, k = i, 2.
2.44 Develop a computer program using Ditlevsen’s expansion for estimating the multivariate normal probability.
2.45 ![]()
Develop computer programs for multivariate normal probability bounds by Rack – witz’s procedure and Ditlevsen’s procedure, respectively.
Abramowitz, M., andStegun, I. A., eds. (i972). Handbook of Mathematical Functions with Formulas,







![Determination of bounds on multivariate normal probability Подпись: i = [4], [5], ...,[K ] i = [4], [5], ...,[K ]](/img/1312/image329_0.png)
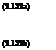
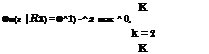




 (CDX) is made from thin layers of fir or other common softwoods glued together with a waterproof glue so it can be used on the building exterior.
(CDX) is made from thin layers of fir or other common softwoods glued together with a waterproof glue so it can be used on the building exterior.

 wood strip (called a web) glued into flanges at top and bottom (see the photo on p. 67). These joists are lightweight and can span long distances, making it possible to create very large rooms. Also, they are always straight and don’t shrink as much as 2x joists, so floors tend to remain flat, level, and relatively squeak free.
wood strip (called a web) glued into flanges at top and bottom (see the photo on p. 67). These joists are lightweight and can span long distances, making it possible to create very large rooms. Also, they are always straight and don’t shrink as much as 2x joists, so floors tend to remain flat, level, and relatively squeak free. Windows When I first started building, we had basically one choice for windows: wood framed. Although wood-framed windows are still around, other options are available now in a wide variety of styles.
Windows When I first started building, we had basically one choice for windows: wood framed. Although wood-framed windows are still around, other options are available now in a wide variety of styles.

 Rights-of-way are publicly-owned land on which streets, sidewalks, curbs, and gutters are built, and which often accommodate utilities such as water, sewer, and electrical service. The government body that owns the right – of-way grants the right of use and passage to the public, or to designated parties such as utilities, under conditions specified by the government. Right-of-way land is not on the property tax rolls and generates no tax income.
Rights-of-way are publicly-owned land on which streets, sidewalks, curbs, and gutters are built, and which often accommodate utilities such as water, sewer, and electrical service. The government body that owns the right – of-way grants the right of use and passage to the public, or to designated parties such as utilities, under conditions specified by the government. Right-of-way land is not on the property tax rolls and generates no tax income.
 The basic facility that must be accommodated by a right-of-way is the roadway with its associated shoulders, curbs, and gutters. As discussed below, traditional designs often resulted in streets much wider than were necessary. This was done for two reasons:
The basic facility that must be accommodated by a right-of-way is the roadway with its associated shoulders, curbs, and gutters. As discussed below, traditional designs often resulted in streets much wider than were necessary. This was done for two reasons:
 State highway standards often serve as a basis for local street standards. However, traffic characteristics, _ construction and maintenance requirements, and performance needs of residential streets differ from those of highways. Reductions in cost and in land use can be achieved by
State highway standards often serve as a basis for local street standards. However, traffic characteristics, _ construction and maintenance requirements, and performance needs of residential streets differ from those of highways. Reductions in cost and in land use can be achieved by Local construction standards often specify a minimum pavement width of 30 to 36 feet, an excessive amount of space for most residential streets. Depending on such factors as speed limit, parking requirements, and lane width, street pavement widths can be reduced to as narrow as 18 feet.
Local construction standards often specify a minimum pavement width of 30 to 36 feet, an excessive amount of space for most residential streets. Depending on such factors as speed limit, parking requirements, and lane width, street pavement widths can be reduced to as narrow as 18 feet.



 In addition to savings from adoption of functional construction criteria, other savings can be achieved through modification of certain features of layout and design.
In addition to savings from adoption of functional construction criteria, other savings can be achieved through modification of certain features of layout and design.

