The horizontal alignment of a roadway should be designed to provide motorists with a facility for driving in a safe and comfortable manner. Adequate stopping sight distance should be furnished. Also, changes in direction should be accompanied by the use of curves and superelevation when appropriate in accordance with established guidelines. Some changes in alignment are slight and may not require curvature. Table 2.5 lists the maximum deflection angle which may be permitted without the use of a horizontal curve for each design speed shown. It is assumed that a motorist can easily negotiate the change in direction and maintain control over the vehicle without leaving the lane.
TABLE 2.4 Decision Sight Distance (DSD) for Design Speeds from 30 to 70 mi/h (48 to 113 km/h)
Decision sight distance, ft
Avoidance maneuver
|
Design speed, mi/h
|
A
|
B
|
C
|
D
|
E
|
|
30
|
220
|
490
|
450
|
535
|
620
|
|
35
|
275
|
590
|
525
|
625
|
720
|
|
40
|
330
|
690
|
600
|
715
|
825
|
|
45
|
395
|
800
|
675
|
800
|
930
|
|
50
|
465
|
910
|
750
|
890
|
1030
|
|
55
|
535
|
1030
|
865
|
980
|
1135
|
|
60
|
610
|
1150
|
990
|
1125
|
1280
|
|
65
|
695
|
1275
|
1050
|
1220
|
1365
|
|
70
|
780
|
1410
|
1105
|
1275
|
1445
|
• The avoidance maneuvers are as follows: A—rural stop; B—urban stop; C—rural speed/path/direction change; D—suburban speed/path/direction change; E—urban speed/path/direction change
• Decision sight distance (DSD) is calculated or measured using the same criteria as stopping sight distance: 3.50 ft (1.07 m) eye height and 2.00 ft (0.61 m) object height.
Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.
Source: Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of
Transportation, with permission.
|
TABLE 2.5 Maximum Centerline Deflection Not Requiring a Horizontal Curve
Design speed, mi/h Maximum deflection*
|
25
|
5°30′
|
|
30
|
3°45′
|
|
35
|
2°45′
|
|
40
|
2°15′
|
|
45
|
1°45′
|
|
50
|
1°15′
|
|
55
|
1°00′
|
|
60
|
1°00′
|
|
65
|
0°45′
|
|
70
|
0°45′
|
|
Based on the following formulas:
Design speed 50 mi/h or over: tan A = 1.0/V Design speed under 50 mi/h: tan A = 60/V2
|
where V = design speed, mi/h A = deflection angle
|
Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.
Note: The recommended minimum distance between consecutive horizontal deflections is:
200 ft where design speed > 45 mi/h 100 ft where design speed < 45 mi/h *Rounded to nearest 15 min.
Source: Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with permission.
When centerline deflections exceed the values in Table 2.5, it is necessary to introduce a horizontal curve to assist the driver. Curves are usually accompanied by superelevation, which is a banking of the roadway to help counteract the effect of centrifugal force on the vehicle as it moves through the curve. In addition to superelevation, centrifugal force is also offset by the side friction developed between the tires of the vehicle and the pavement surface. The relationship of the two factors when considering curvature for a particular design speed is expressed by the following equation:
|
U. S. units: e + f =
|
V2 15V
|
(2.1a)
|
|
SI units: e + f =
|
V2
127R
|
(2.1b)
|
where e = superelevation rate, ft per ft (m per m) of pavement width f = side friction factor V = design speed, mi/h (km/h)
R = radius of curve, ft (m)
In developing superelevation guidelines for use in designing roadways, it is necessary to establish practical limits for both superelevation and side friction factors. Several factors affect the selection of a maximum superelevation rate for a given highway. Climate must be considered. Regions subject to snow and ice should not be superelevated too sharply, because the presence of these adverse conditions causes motorists to drive slower, and side friction is greatly reduced. Consequently, vehicles tend to slide to the low side of the roadway. Terrain conditions are another factor. Flat areas tend to have relatively flat grades, and such conditions have little effect on superelevation and side friction factors. However, mountainous regions have steeper grades, which combine with superelevation rates to produce steeper cross slopes on the pavement than may be apparent to the designer. Rural and urban areas require different maximum superelevation rates, because urban areas are more frequently subjected to congestion and slower-moving traffic. Vehicles operating at significantly less than design speeds necessitate a flatter maximum rate. Given the above considerations, a range of maximum values has been adopted for use in design. A maximum rate of 0.12 or 0.10 may be used in flat areas not subject to ice or snow. Rural areas where these conditions exist usually have a maximum rate of 0.08. A maximum rate of 0.06 is recommended for urban high-speed roadways, 50 mi/h (80 km/h) or greater, while 0.04 is used on low-speed urban roadways and temporary roads.
Various factors affect the side friction factors used in design. Among these are pavement texture, weather conditions, and tire condition. The upper limit of the side friction factor is when the tires begin to skid. Highway curves must be designed to avoid skidding conditions with a margin of safety. Side friction factors also vary with design speed. Higher speeds tend to have lower side friction factors. The result of various studies leads to the values listed in Table 2.6, which shows the side friction factors by design speed generally used in developing superelevation tables (Ref. 1).
Taking into account the above limits on superelevation rates and side friction factors, and rewriting Eq. (2.1), it follows that for a given design speed and maximum superelevation rate, there exists a minimum radius of curvature that should be allowed for design purposes:
V2
R. = ————— (2.2)
mn 15(e + f) v ‘
To allow a lesser radius for the design speed would require the superelevation rate or the friction factor to be increased beyond the recommended limit.
Highway design using U. S. Customary units defines horizontal curvature in terms of degree of curve as well as radius. Under this definition, the degree of curve is defined as the central angle of a 100-ft (30-m) arc using a fixed radius. This results in the following equation relating R (radius, ft) to D (degree of curve, degrees):
 5729.6
5729.6
R
Substituting in Eq. (2.2) gives the maximum degree of curvature for a given design speed and maximum superelevation rate:
Before presenting the superelevation tables, one final consideration must be addressed. Because for any curve, superelevation and side friction combine to offset the effects of centrifugal force, the question arises how much superelevation should be provided for curves flatter than the “maximum” allowed for a given design speed. The following five methods have been used over the years (Ref. 1):
Method 1. Superelevation and side friction are directly proportional to the degree of curve or the inverse of the radius.
Method 2. Side friction is used to offset centrifugal force in direct proportion to the degree of curve, for curves up to the point where fmax is required. For sharper curves, fmax remains constant and e is increased in direct proportion to the increasing degree of curvature until e is reached.
Method 3. Superelevation is used to offset centrifugal force in direct proportion to the degree of curve for curves up to the point where emax is required. For sharper curves, emax remains constant and f is increased in direct proportion to the increasing degree of curvature until f is reached.
Method 4. Method 4 is similar to method 3, except that it is based on average running speed instead of design speed.
Method 5. Superelevation and side friction are in a curvilinear relationship with the degree of curve (inverse of radius), with resulting values between those of method 1 and method 3.
Figure 2.8 shows a graphic comparison of the various methods. Method 5 is most commonly used on rural and high-speed [50 mi/h (80 km/h) or higher] urban highways. Method 2 is used on low-speed urban streets and temporary roadways.
Recommended minimum radii for a given range of design speeds and incremental superelevation rates are given in Tables 2.7 through 2.11, where each table represents
|
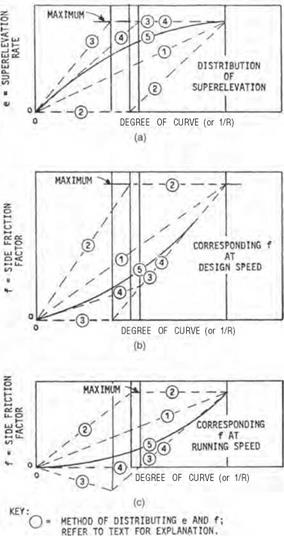
FIGURE 2.8 Methods of distributing superelevation and side friction. (a) Superelevation. (b) Corresponding friction factor at design speed. (c) Corresponding friction factor at running speed. (From A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission)
|
|
TABLE 2.7 Minimum Radii for Design Speeds from 15 to 60 mi/ti (24 to 97 km/h) and Superelevation Rates to 4 Percent
|
e
(%)
|
V, = 15 mi/h
a
R (ft)
|
V. = 20 mi/h
a
R (ft)
|
V, = 25 mi/h
a
R (ft)
|
V, = 30 mi/h
a
R (ft)
|
V. = 35 mi/h
a
R (ft)
|
V. = 40 mi/h
a
Я (ft)
|
V. = 45 mi/h
a
R (ft)
|
V, = 50 mi/h
a
R (ft)
|
V. = 55 mi/h
a
R (ft)
|
V. = 60 mi/h
a
R (ft)
|
|
1.5
|
796
|
1410
|
2050
|
2830
|
3730
|
4770
|
5930
|
7220
|
8650
|
10300
|
|
2.0
|
506
|
902
|
1340
|
1880
|
2490
|
3220
|
4040
|
4940
|
5950
|
7080
|
|
2.2
|
399
|
723
|
1110
|
1580
|
2120
|
2760
|
3480
|
4280
|
5180
|
6190
|
|
2.4
|
271
|
513
|
838
|
1270
|
1760
|
2340
|
2980
|
3690
|
4500
|
5410
|
|
2.6
|
201
|
388
|
650
|
1000
|
1420
|
1930
|
2490
|
3130
|
3870
|
4700
|
|
2.8
|
157
|
308
|
524
|
817
|
1170
|
1620
|
2100
|
2660
|
3310
|
4060
|
|
3.0
|
127
|
251
|
433
|
681
|
982
|
1370
|
1800
|
2290
|
2860
|
3530
|
|
3.2
|
105
|
209
|
363
|
576
|
835
|
1180
|
1550
|
1980
|
2490
|
3090
|
|
3.4
|
88
|
175
|
307
|
490
|
714
|
1010
|
1340
|
1720
|
2170
|
2700
|
|
3.6
|
73
|
147
|
259
|
416
|
610
|
865
|
1150
|
1480
|
1880
|
2350
|
|
3.8
|
61
|
122
|
215
|
348
|
512
|
730
|
970
|
1260
|
1600
|
2010
|
|
4.0
|
42
|
86
|
154
|
250
|
371
|
533
|
711
|
926
|
1190
|
1500
|
Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.
R = radius of curve Vd = design speed e = rate of superelevation
Note: Use of emax = 4 percent should be limited to urban conditions.
Source: A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission.
|
|
TABLE 2.8 Minimum Radii for Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 6 Percent
|
e
(%)
|
Vd = 15 mi/h R (ft)
|
Vd = 20 mi/h R (ft)
|
Vd = 25 mi/h R (ft)
|
Vd = 30 mi/h R (ft)
|
Vd = 35 mi/h R (ft)
|
Vd = 40 mi/h R (ft)
|
Vd = 45 mi/h R (ft)
|
|
1.5
|
868
|
1580
|
2290
|
3130
|
4100
|
5230
|
6480
|
|
2.0
|
614
|
1120
|
1630
|
2240
|
2950
|
3770
|
4680
|
|
2.2
|
543
|
991
|
1450
|
2000
|
2630
|
3370
|
4190
|
|
2.4
|
482
|
884
|
1300
|
1790
|
2360
|
3030
|
3770
|
|
2.6
|
430
|
791
|
1170
|
1610
|
2130
|
2740
|
3420
|
|
2.8
|
384
|
709
|
1050
|
1460
|
1930
|
2490
|
3110
|
|
3.0
|
341
|
635
|
944
|
1320
|
1760
|
2270
|
2840
|
|
3.2
|
300
|
566
|
850
|
1200
|
1600
|
2080
|
2600
|
|
3.4
|
256
|
498
|
761
|
1080
|
1460
|
1900
|
2390
|
|
3.6
|
209
|
422
|
673
|
972
|
1320
|
1740
|
2190
|
|
3.8
|
176
|
358
|
583
|
864
|
1190
|
1590
|
2010
|
|
4.0
|
151
|
309
|
511
|
766
|
1070
|
1440
|
1840
|
|
4.2
|
131
|
270
|
452
|
684
|
960
|
1310
|
1680
|
|
4.4
|
116
|
238
|
402
|
615
|
868
|
1190
|
1540
|
|
4.6
|
102
|
212
|
360
|
555
|
788
|
1090
|
1410
|
|
4.8
|
91
|
189
|
324
|
502
|
718
|
995
|
1300
|
|
5.0
|
82
|
169
|
292
|
456
|
654
|
911
|
1190
|
|
5.2
|
73
|
152
|
264
|
413
|
595
|
833
|
1090
|
|
5.4
|
65
|
136
|
237
|
373
|
540
|
759
|
995
|
|
5.6
|
58
|
121
|
212
|
335
|
487
|
687
|
903
|
|
5.8
|
51
|
106
|
186
|
296
|
431
|
611
|
806
|
|
6.0
|
39
|
81
|
144
|
231
|
340
|
485
|
643
|
(Continued)
|
|
e
|
Vd = 50 mi/h
|
Vd = 55 mi/h
|
II
o
о
3
&
|
Vd = 65 mi/h
|
Vd = 70 mi/h
|
Vd = 75 mi/h
|
Vd = 80 mi/h
|
|
(%)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
|
1.5
|
7870
|
9410
|
11100
|
12600
|
14100
|
15700
|
17400
|
|
2.0
|
5700
|
6820
|
8060
|
9130
|
10300
|
11500
|
12900
|
|
2.2
|
5100
|
6110
|
7230
|
8200
|
9240
|
10400
|
11600
|
|
2.4
|
4600
|
5520
|
6540
|
7430
|
8380
|
9420
|
10600
|
|
2.6
|
4170
|
5020
|
5950
|
6770
|
7660
|
8620
|
9670
|
|
2.8
|
3800
|
4580
|
5440
|
6200
|
7030
|
7930
|
8910
|
|
3.0
|
3480
|
4200
|
4990
|
5710
|
6490
|
7330
|
8260
|
|
3.2
|
3200
|
3860
|
4600
|
5280
|
6010
|
6810
|
7680
|
|
3.4
|
2940
|
3560
|
4250
|
4890
|
5580
|
6340
|
7180
|
|
3.6
|
2710
|
3290
|
3940
|
4540
|
5210
|
5930
|
6720
|
|
3.8
|
2490
|
3040
|
3650
|
4230
|
4860
|
5560
|
6320
|
|
4.0
|
2300
|
2810
|
3390
|
3950
|
4550
|
5220
|
5950
|
|
4.2
|
2110
|
2590
|
3140
|
3680
|
4270
|
4910
|
5620
|
|
4.4
|
1940
|
2400
|
2920
|
3440
|
4010
|
4630
|
5320
|
|
4.6
|
1780
|
2210
|
2710
|
3220
|
3770
|
4380
|
5040
|
|
4.8
|
1640
|
2050
|
2510
|
3000
|
3550
|
4140
|
4790
|
|
5.0
|
1510
|
1890
|
2330
|
2800
|
3330
|
3910
|
4550
|
|
5.2
|
1390
|
1750
|
2160
|
2610
|
3120
|
3690
|
4320
|
|
5.4
|
1280
|
1610
|
1990
|
2420
|
2910
|
3460
|
4090
|
|
5.6
|
1160
|
1470
|
1830
|
2230
|
2700
|
3230
|
3840
|
|
5.8
|
1040
|
1320
|
1650
|
2020
|
2460
|
2970
|
3560
|
|
6.0
|
833
|
1060
|
1330
|
1660
|
2040
|
2500
|
3050
|
Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.
R = radius of curve Vd = design speed e = rate of superelevation
Source: A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission.
|
TABLE 2.9 Minimum Radii for Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 8 Percent
|
e
|
Vd = 15 mi/h Vd
|
= 20 mi/h
|
Vd = 25 mi/h Vd
|
= 30 mi/h
|
Vd = 35 mi/h
|
II
4^
О
3
&
|
Vd = 45 mi/h
|
|
(%)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
|
1.5
|
932
|
1640
|
2370
|
3240
|
4260
|
5410
|
6710
|
|
2.0
|
676
|
1190
|
1720
|
2370
|
3120
|
3970
|
4930
|
|
2.2
|
605
|
1070
|
1550
|
2130
|
2800
|
3570
|
4440
|
|
2.4
|
546
|
959
|
1400
|
1930
|
2540
|
3240
|
4030
|
|
2.6
|
496
|
872
|
1280
|
1760
|
2320
|
2960
|
3690
|
|
2.8
|
453
|
796
|
1170
|
1610
|
2130
|
2720
|
3390
|
|
3.0
|
415
|
730
|
1070
|
1480
|
1960
|
2510
|
3130
|
|
3.2
|
382
|
672
|
985
|
1370
|
1820
|
2330
|
2900
|
|
3.4
|
352
|
620
|
911
|
1270
|
1690
|
2170
|
2700
|
|
3.6
|
324
|
572
|
845
|
1180
|
1570
|
2020
|
2520
|
|
3.8
|
300
|
530
|
784
|
1100
|
1470
|
1890
|
2360
|
|
4.0
|
277
|
490
|
729
|
1030
|
1370
|
1770
|
2220
|
|
4.2
|
255
|
453
|
678
|
955
|
1280
|
1660
|
2080
|
|
4.4
|
235
|
418
|
630
|
893
|
1200
|
1560
|
1960
|
|
4.6
|
215
|
384
|
585
|
834
|
1130
|
1470
|
1850
|
|
4.8
|
193
|
349
|
542
|
779
|
1060
|
1390
|
1750
|
|
5.0
|
172
|
314
|
499
|
727
|
991
|
1310
|
1650
|
|
5.2
|
154
|
284
|
457
|
676
|
929
|
1230
|
1560
|
|
5.4
|
139
|
258
|
420
|
627
|
870
|
1160
|
1480
|
|
5.6
|
126
|
236
|
387
|
582
|
813
|
1090
|
1390
|
|
5.8
|
115
|
216
|
358
|
542
|
761
|
1030
|
1320
|
|
6.0
|
105
|
199
|
332
|
506
|
713
|
965
|
1250
|
|
6.2
|
97
|
184
|
308
|
472
|
669
|
909
|
1180
|
|
6.4
|
89
|
170
|
287
|
442
|
628
|
857
|
1110
|
|
6.6
|
82
|
157
|
267
|
413
|
590
|
808
|
1050
|
|
6.8
|
76
|
146
|
248
|
386
|
553
|
761
|
990
|
|
7.0
|
70
|
135
|
231
|
360
|
518
|
716
|
933
|
|
7.2
|
64
|
125
|
214
|
336
|
485
|
672
|
878
|
|
7.4
|
59
|
115
|
198
|
312
|
451
|
628
|
822
|
|
7.6
|
54
|
105
|
182
|
287
|
417
|
583
|
765
|
|
7.8
|
48
|
94
|
164
|
261
|
380
|
533
|
701
|
|
8.0
|
38
|
76
|
134
|
214
|
314
|
444
|
587
|
|
|
e
|
Vd = 50 mi/h
|
Vd = 55 mi/h
|
II
C
О
3
&
|
Vd = 65 mi/h
|
Vd = 70 mi/h
|
Vd = 75 mi/h
|
Vd = 80 mi/h
|
|
(%)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
|
1.5
|
8150
|
9720
|
11500
|
12900
|
14500
|
16100
|
17800
|
|
2.0
|
5990
|
7150
|
8440
|
9510
|
10700
|
12000
|
13300
|
|
2.2
|
5400
|
6450
|
7620
|
8600
|
9660
|
10800
|
12000
|
|
2.4
|
4910
|
5870
|
6930
|
7830
|
8810
|
9850
|
11000
|
|
2.6
|
4490
|
5370
|
6350
|
7180
|
8090
|
9050
|
10100
|
|
2.8
|
4130
|
4950
|
5850
|
6630
|
7470
|
8370
|
9340
|
|
3.0
|
3820
|
4580
|
5420
|
6140
|
6930
|
7780
|
8700
|
|
3.2
|
3550
|
4250
|
5040
|
5720
|
6460
|
7260
|
8130
|
|
3.4
|
3300
|
3970
|
4700
|
5350
|
6050
|
6800
|
7620
|
|
3.6
|
3090
|
3710
|
4400
|
5010
|
5680
|
6400
|
7180
|
|
3.8
|
2890
|
3480
|
4140
|
4710
|
5350
|
6030
|
6780
|
|
4.0
|
2720
|
3270
|
3890
|
4450
|
5050
|
5710
|
6420
|
|
4.2
|
2560
|
3080
|
3670
|
4200
|
4780
|
5410
|
6090
|
|
4.4
|
2410
|
2910
|
3470
|
3980
|
4540
|
5140
|
5800
|
|
4.6
|
2280
|
2750
|
3290
|
3770
|
4310
|
4890
|
5530
|
|
4.8
|
2160
|
2610
|
3120
|
3590
|
4100
|
4670
|
5280
|
|
5.0
|
2040
|
2470
|
2960
|
3410
|
3910
|
4460
|
5050
|
|
5.2
|
1930
|
2350
|
2820
|
3250
|
3740
|
4260
|
4840
|
|
5.4
|
1830
|
2230
|
2680
|
3110
|
3570
|
4090
|
4640
|
|
5.6
|
1740
|
2120
|
2550
|
2970
|
3420
|
3920
|
4460
|
|
5.8
|
1650
|
2010
|
2430
|
2840
|
3280
|
3760
|
4290
|
|
6.0
|
1560
|
1920
|
2320
|
2710
|
3150
|
3620
|
4140
|
|
6.2
|
1480
|
1820
|
2210
|
2600
|
3020
|
3480
|
3990
|
|
6.4
|
1400
|
1730
|
2110
|
2490
|
2910
|
3360
|
3850
|
|
6.6
|
1330
|
1650
|
2010
|
2380
|
2790
|
3240
|
3720
|
|
6.8
|
1260
|
1560
|
1910
|
2280
|
2690
|
3120
|
3600
|
|
7.0
|
1190
|
1480
|
1820
|
2180
|
2580
|
3010
|
3480
|
|
7.2
|
1120
|
1400
|
1720
|
2070
|
2470
|
2900
|
3370
|
|
7.4
|
1060
|
1320
|
1630
|
1970
|
2350
|
2780
|
3250
|
|
7.6
|
980
|
1230
|
1530
|
1850
|
2230
|
2650
|
3120
|
|
7.8
|
901
|
1140
|
1410
|
1720
|
2090
|
2500
|
2970
|
|
8.0
|
758
|
960
|
1200
|
1480
|
1810
|
2210
|
2670
|
|
Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.
R = radius of curve Vd = design speed e = rate of superelevation
Source: A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission.
|
|
TABLE 2.10 Minimum Radii for Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 10 Percent
|
e Vd
|
= 15 mi/h Vd
|
= 20 mi/h
|
Vd = 25 mi/h Vd
|
= 30 mi/h
|
Vd = 35 mi/h
|
II
4^
О
3
&
|
Vd = 45 mi/h
|
|
(%)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
|
1.5
|
947
|
1680
|
2420
|
3320
|
4350
|
5520
|
6830
|
|
2.0
|
694
|
1230
|
1780
|
2440
|
3210
|
4080
|
5050
|
|
2.2
|
625
|
1110
|
1600
|
2200
|
2900
|
3680
|
4570
|
|
2.4
|
567
|
1010
|
1460
|
2000
|
2640
|
3350
|
4160
|
|
2.6
|
517
|
916
|
1330
|
1840
|
2420
|
3080
|
3820
|
|
2.8
|
475
|
841
|
1230
|
1690
|
2230
|
2840
|
3520
|
|
3.0
|
438
|
777
|
1140
|
1570
|
2060
|
2630
|
3270
|
|
3.2
|
406
|
720
|
1050
|
1450
|
1920
|
2450
|
3040
|
|
3.4
|
377
|
670
|
978
|
1360
|
1790
|
2290
|
2850
|
|
3.6
|
352
|
625
|
913
|
1270
|
1680
|
2150
|
2670
|
|
3.8
|
329
|
584
|
856
|
1190
|
1580
|
2020
|
2510
|
|
4.0
|
308
|
547
|
804
|
1120
|
1490
|
1900
|
2370
|
|
4.2
|
289
|
514
|
756
|
1060
|
1400
|
1800
|
2240
|
|
4.4
|
271
|
483
|
713
|
994
|
1330
|
1700
|
2120
|
|
4.6
|
255
|
455
|
673
|
940
|
1260
|
1610
|
2020
|
|
4.8
|
240
|
429
|
636
|
890
|
1190
|
1530
|
1920
|
|
5.0
|
226
|
404
|
601
|
844
|
1130
|
1460
|
1830
|
|
5.2
|
213
|
381
|
569
|
802
|
1080
|
1390
|
1740
|
|
5.4
|
200
|
359
|
539
|
762
|
1030
|
1330
|
1660
|
|
5.6
|
188
|
339
|
511
|
724
|
974
|
1270
|
1590
|
|
5.8
|
176
|
319
|
484
|
689
|
929
|
1210
|
1520
|
|
6.0
|
164
|
299
|
458
|
656
|
886
|
1160
|
1460
|
|
6.2
|
152
|
280
|
433
|
624
|
846
|
1110
|
1400
|
|
6.4
|
140
|
260
|
409
|
594
|
808
|
1060
|
1340
|
|
6.6
|
130
|
242
|
386
|
564
|
772
|
1020
|
1290
|
|
6.8
|
120
|
226
|
363
|
536
|
737
|
971
|
1230
|
|
7.0
|
112
|
212
|
343
|
509
|
704
|
931
|
1190
|
|
7.2
|
105
|
199
|
324
|
483
|
671
|
892
|
1140
|
|
7.4
|
98
|
187
|
306
|
460
|
641
|
855
|
1100
|
|
7.6
|
92
|
176
|
290
|
437
|
612
|
820
|
1050
|
|
7.8
|
86
|
165
|
274
|
416
|
585
|
786
|
1010
|
|
8.0
|
81
|
156
|
260
|
396
|
558
|
754
|
968
|
|
8.2
|
76
|
147
|
246
|
377
|
533
|
722
|
930
|
|
8.4
|
72
|
139
|
234
|
359
|
509
|
692
|
893
|
|
8.6
|
68
|
131
|
221
|
341
|
486
|
662
|
856
|
|
8.8
|
64
|
124
|
209
|
324
|
463
|
633
|
820
|
|
9.0
|
60
|
116
|
198
|
307
|
440
|
604
|
784
|
|
9.2
|
56
|
109
|
186
|
291
|
418
|
574
|
748
|
|
9.4
|
52
|
102
|
175
|
274
|
395
|
545
|
710
|
|
9.6
|
48
|
95
|
163
|
256
|
370
|
513
|
671
|
|
9.8
|
44
|
87
|
150
|
236
|
343
|
477
|
625
|
|
10.0
|
36
|
72
|
126
|
200
|
292
|
410
|
540
|
(Continued)
|
|
e Vd
|
= 50 mi/h
|
Vd = 55 mi/h
|
II
o
О
3
&
|
Vd = 65 mi/h
|
Vd = 70 mi/h
|
Vd = 75 mi/h
|
Vd = 80 mi/h
|
|
(%)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
|
1.5
|
8280
|
9890
|
11700
|
13100
|
14700
|
16300
|
18000
|
|
2.0
|
6130
|
7330
|
8630
|
9720
|
10900
|
12200
|
13500
|
|
2.2
|
5540
|
6630
|
7810
|
8800
|
9860
|
11000
|
12200
|
|
2.4
|
5050
|
6050
|
7130
|
8040
|
9010
|
10100
|
11200
|
|
2.6
|
4640
|
5550
|
6550
|
7390
|
8290
|
9260
|
10300
|
|
2.8
|
4280
|
5130
|
6050
|
6840
|
7680
|
8580
|
9550
|
|
3.0
|
3970
|
4760
|
5620
|
6360
|
7140
|
7990
|
8900
|
|
3.2
|
3700
|
4440
|
5250
|
5930
|
6680
|
7480
|
8330
|
|
3.4
|
3470
|
4160
|
4910
|
5560
|
6260
|
7020
|
7830
|
|
3.6
|
3250
|
3900
|
4620
|
5230
|
5900
|
6620
|
7390
|
|
3.8
|
3060
|
3680
|
4350
|
4940
|
5570
|
6260
|
6990
|
|
4.0
|
2890
|
3470
|
4110
|
4670
|
5270
|
5930
|
6630
|
|
4.2
|
2740
|
3290
|
3900
|
4430
|
5010
|
5630
|
6300
|
|
4.4
|
2590
|
3120
|
3700
|
4210
|
4760
|
5370
|
6010
|
|
4.6
|
2460
|
2970
|
3520
|
4010
|
4540
|
5120
|
5740
|
|
4.8
|
2340
|
2830
|
3360
|
3830
|
4340
|
4900
|
5490
|
|
5.0
|
2240
|
2700
|
3200
|
3660
|
4150
|
4690
|
5270
|
|
5.2
|
2130
|
2580
|
3060
|
3500
|
3980
|
4500
|
5060
|
|
5.4
|
2040
|
2460
|
2930
|
3360
|
3820
|
4320
|
4860
|
|
5.6
|
1950
|
2360
|
2810
|
3220
|
3670
|
4160
|
4680
|
|
5.8
|
1870
|
2260
|
2700
|
3090
|
3530
|
4000
|
4510
|
|
6.0
|
1790
|
2170
|
2590
|
2980
|
3400
|
3860
|
4360
|
|
6.2
|
1720
|
2090
|
2490
|
2870
|
3280
|
3730
|
4210
|
|
6.4
|
1650
|
2010
|
2400
|
2760
|
3160
|
3600
|
4070
|
|
6.6
|
1590
|
1930
|
2310
|
2670
|
3060
|
3480
|
3940
|
|
6.8
|
1530
|
1860
|
2230
|
2570
|
2960
|
3370
|
3820
|
|
7.0
|
1470
|
1790
|
2150
|
2490
|
2860
|
3270
|
3710
|
|
7.2
|
1410
|
1730
|
2070
|
2410
|
2770
|
3170
|
3600
|
|
7.4
|
1360
|
1670
|
2000
|
2330
|
2680
|
3070
|
3500
|
|
7.6
|
1310
|
1610
|
1940
|
2250
|
2600
|
2990
|
3400
|
|
7.8
|
1260
|
1550
|
1870
|
2180
|
2530
|
2900
|
3310
|
|
8.0
|
1220
|
1500
|
1810
|
2120
|
2450
|
2820
|
3220
|
|
8.2
|
1170
|
1440
|
1750
|
2050
|
2380
|
2750
|
3140
|
|
8.4
|
1130
|
1390
|
1690
|
1990
|
2320
|
2670
|
3060
|
|
8.6
|
1080
|
1340
|
1630
|
1930
|
2250
|
2600
|
2980
|
|
8.8
|
1040
|
1290
|
1570
|
1870
|
2190
|
2540
|
2910
|
|
9.0
|
992
|
1240
|
1520
|
1810
|
2130
|
2470
|
2840
|
|
9.2
|
948
|
1190
|
1460
|
1740
|
2060
|
2410
|
2770
|
|
9.4
|
903
|
1130
|
1390
|
1670
|
1990
|
2340
|
2710
|
|
9.6
|
854
|
1080
|
1320
|
1600
|
1910
|
2260
|
2640
|
|
9.8
|
798
|
1010
|
1250
|
1510
|
1820
|
2160
|
2550
|
|
10.0
|
694
|
877
|
1090
|
1340
|
1630
|
1970
|
2370
|
Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.
R = radius of curve Vd = design speed e = rate of Superelevation
Source: A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission.
|
TABLE 2.11 Minimum Radii for Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 12 Percent
|
e
|
Vd = 15 mi/h Vd
|
= 20 mi/h
|
Vd = 25 mi/h Vd
|
= 30 mi/h
|
Vd = 35 mi/h
|
II
О
3
|
Vd = 45 mi/h
|
|
(%)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
|
1.5
|
950
|
1690
|
2460
|
3370
|
4390
|
5580
|
6910
|
|
2.0
|
700
|
1250
|
1820
|
2490
|
3260
|
4140
|
5130
|
|
2.2
|
631
|
1130
|
1640
|
2250
|
2950
|
3750
|
4640
|
|
2.4
|
574
|
1030
|
1500
|
2060
|
2690
|
3420
|
4240
|
|
2.6
|
526
|
936
|
1370
|
1890
|
2470
|
3140
|
3900
|
|
2.8
|
484
|
863
|
1270
|
1740
|
2280
|
2910
|
3600
|
|
3.0
|
448
|
799
|
1170
|
1620
|
2120
|
2700
|
3350
|
|
3.2
|
417
|
743
|
1090
|
1510
|
1970
|
2520
|
3130
|
|
3.4
|
389
|
693
|
1020
|
1410
|
1850
|
2360
|
2930
|
|
3.6
|
364
|
649
|
953
|
1320
|
1730
|
2220
|
2750
|
|
3.8
|
341
|
610
|
896
|
1250
|
1630
|
2090
|
2600
|
|
4.0
|
321
|
574
|
845
|
1180
|
1540
|
1980
|
2460
|
|
4.2
|
303
|
542
|
798
|
1110
|
1460
|
1870
|
2330
|
|
4.4
|
286
|
512
|
756
|
1050
|
1390
|
1780
|
2210
|
|
4.6
|
271
|
485
|
717
|
997
|
1320
|
1690
|
2110
|
|
4.8
|
257
|
460
|
681
|
948
|
1260
|
1610
|
2010
|
|
5.0
|
243
|
437
|
648
|
904
|
1200
|
1540
|
1920
|
|
5.2
|
231
|
415
|
618
|
862
|
1140
|
1470
|
1840
|
|
5.4
|
220
|
395
|
589
|
824
|
1090
|
1410
|
1760
|
|
5.6
|
209
|
377
|
563
|
788
|
1050
|
1350
|
1690
|
|
5.8
|
199
|
359
|
538
|
754
|
1000
|
1300
|
1620
|
|
6.0
|
190
|
343
|
514
|
723
|
960
|
1250
|
1560
|
|
6.2
|
181
|
327
|
492
|
694
|
922
|
1200
|
1500
|
|
6.4
|
172
|
312
|
471
|
666
|
886
|
1150
|
1440
|
|
6.6
|
164
|
298
|
452
|
639
|
852
|
1110
|
1390
|
|
6.8
|
156
|
284
|
433
|
615
|
820
|
1070
|
1340
|
|
7.0
|
148
|
271
|
415
|
591
|
790
|
1030
|
1300
|
|
7.2
|
140
|
258
|
398
|
568
|
762
|
994
|
1250
|
|
7.4
|
133
|
246
|
382
|
547
|
734
|
960
|
1210
|
|
7.6
|
125
|
234
|
366
|
527
|
708
|
928
|
1170
|
|
7.8
|
118
|
222
|
351
|
507
|
684
|
897
|
1130
|
|
8.0
|
111
|
210
|
336
|
488
|
660
|
868
|
1100
|
|
|
e Vd
|
= 15 mi/h
|
Vd = 20 mi/h
|
Vd = 25 mi/h
|
Vd = 30 mi/h
|
Vd = 35 mi/h
|
II
4^
О
3
&
|
Vd = 45 mi/h
|
|
(%)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
|
8.2
|
105
|
199
|
321
|
470
|
637
|
840
|
1070
|
|
8.4
|
100
|
190
|
307
|
452
|
615
|
813
|
1030
|
|
8.6
|
95
|
180
|
294
|
435
|
594
|
787
|
997
|
|
8.8
|
90
|
172
|
281
|
418
|
574
|
762
|
967
|
|
9.0
|
85
|
164
|
270
|
403
|
554
|
738
|
938
|
|
9.2
|
81
|
156
|
259
|
388
|
535
|
715
|
910
|
|
9.4
|
77
|
149
|
248
|
373
|
516
|
693
|
883
|
|
9.6
|
74
|
142
|
238
|
359
|
499
|
671
|
857
|
|
9.8
|
70
|
136
|
228
|
346
|
481
|
650
|
832
|
|
10.0
|
67
|
130
|
219
|
333
|
465
|
629
|
806
|
|
10.2
|
64
|
124
|
210
|
320
|
448
|
608
|
781
|
|
10.4
|
61
|
118
|
201
|
308
|
432
|
588
|
757
|
|
10.6
|
58
|
113
|
192
|
296
|
416
|
568
|
732
|
|
10.8
|
55
|
108
|
184
|
284
|
400
|
548
|
707
|
|
11.0
|
52
|
102
|
175
|
272
|
384
|
527
|
682
|
|
11.2
|
49
|
97
|
167
|
259
|
368
|
506
|
656
|
|
11.4
|
47
|
92
|
158
|
247
|
351
|
485
|
629
|
|
11.6
|
44
|
86
|
149
|
233
|
333
|
461
|
600
|
|
11.8
|
40
|
80
|
139
|
218
|
312
|
434
|
566
|
|
12.0
|
34
|
68
|
119
|
188
|
272
|
381
|
500
|
|
TABLE 2.11 Minimum Radii for Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 12 Percent (Continued)
|
e
|
Vd = 50 mi/h Vd
|
= 55 mi/h
|
Vd = 60 mi/h
|
Vd = 65 mi/h
|
Vd = 70 mi/h
|
Vd = 75 mi/h
|
Vd = 80 mi/h
|
|
(%)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
|
1.5
|
8370
|
9990
|
11800
|
13200
|
14800
|
16400
|
18100
|
|
2.0
|
6220
|
7430
|
8740
|
9840
|
11000
|
12300
|
13600
|
|
2.2
|
5640
|
6730
|
7930
|
8920
|
9980
|
11200
|
12400
|
|
2.4
|
5150
|
6150
|
7240
|
8160
|
9130
|
10200
|
11300
|
|
2.6
|
4730
|
5660
|
6670
|
7510
|
8420
|
9380
|
10500
|
|
2.8
|
4380
|
5240
|
6170
|
6960
|
7800
|
8700
|
9660
|
|
3.0
|
4070
|
4870
|
5740
|
6480
|
7270
|
8110
|
9010
|
|
3.2
|
3800
|
4550
|
5370
|
6060
|
6800
|
7600
|
8440
|
|
3.4
|
3560
|
4270
|
5030
|
5690
|
6390
|
7140
|
7940
|
|
3.6
|
3350
|
4020
|
4740
|
5360
|
6020
|
6740
|
7500
|
|
3.8
|
3160
|
3790
|
4470
|
5060
|
5700
|
6380
|
7100
|
|
4.0
|
2990
|
3590
|
4240
|
4800
|
5400
|
6050
|
6740
|
|
4.2
|
2840
|
3400
|
4020
|
4560
|
5130
|
5750
|
6420
|
|
4.4
|
2700
|
3240
|
3830
|
4340
|
4890
|
5490
|
6120
|
|
4.6
|
2570
|
3080
|
3650
|
4140
|
4670
|
5240
|
5850
|
|
4.8
|
2450
|
2940
|
3480
|
3960
|
4470
|
5020
|
5610
|
|
5.0
|
2340
|
2810
|
3330
|
3790
|
4280
|
4810
|
5380
|
|
5.2
|
2240
|
2700
|
3190
|
3630
|
4110
|
4620
|
5170
|
|
5.4
|
2150
|
2590
|
3060
|
3490
|
3950
|
4440
|
4980
|
|
5.6
|
2060
|
2480
|
2940
|
3360
|
3800
|
4280
|
4800
|
|
5.8
|
1980
|
2390
|
2830
|
3230
|
3660
|
4130
|
4630
|
|
6.0
|
1910
|
2300
|
2730
|
3110
|
3530
|
3990
|
4470
|
|
6.2
|
1840
|
2210
|
2630
|
3010
|
3410
|
3850
|
4330
|
|
6.4
|
1770
|
2140
|
2540
|
2900
|
3300
|
3730
|
4190
|
|
6.6
|
1710
|
2060
|
2450
|
2810
|
3190
|
3610
|
4060
|
|
6.8
|
1650
|
1990
|
2370
|
2720
|
3090
|
3500
|
3940
|
|
7.0
|
1590
|
1930
|
2290
|
2630
|
3000
|
3400
|
3820
|
|
7.2
|
1540
|
1860
|
2220
|
2550
|
2910
|
3300
|
3720
|
|
7.4
|
1490
|
1810
|
2150
|
2470
|
2820
|
3200
|
3610
|
|
7.6
|
1440
|
1750
|
2090
|
2400
|
2740
|
3120
|
3520
|
|
7.8
|
1400
|
1700
|
2020
|
2330
|
2670
|
3030
|
3430
|
|
8.0
|
1360
|
1650
|
1970
|
2270
|
2600
|
2950
|
3340
|
|
|
e Vd
|
= 50 mi/h
|
Vd = 55 mi/h
|
Vd = 60 mi/h
|
Vd = 65 mi/h
|
Vd = 70 mi/h
|
Vd = 75 mi/h
|
Vd = 80 mi/h
|
|
(%)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
R (ft)
|
|
8.2
|
1320
|
1600
|
1910
|
2210
|
2530
|
2880
|
3260
|
|
8.4
|
1280
|
1550
|
1860
|
2150
|
2460
|
2800
|
3180
|
|
8.6
|
1240
|
1510
|
1810
|
2090
|
2400
|
2740
|
3100
|
|
8.8
|
1200
|
1470
|
1760
|
2040
|
2340
|
2670
|
3030
|
|
9.0
|
1170
|
1430
|
1710
|
1980
|
2280
|
2610
|
2960
|
|
9.2
|
1140
|
1390
|
1660
|
1940
|
2230
|
2550
|
2890
|
|
9.4
|
1100
|
1350
|
1620
|
1890
|
2180
|
2490
|
2830
|
|
9.6
|
1070
|
1310
|
1580
|
1840
|
2130
|
2440
|
2770
|
|
9.8
|
1040
|
1280
|
1540
|
1800
|
2080
|
2380
|
2710
|
|
10.0
|
1010
|
1250
|
1500
|
1760
|
2030
|
2330
|
2660
|
|
10.2
|
980
|
1210
|
1460
|
1720
|
1990
|
2280
|
2600
|
|
10.4
|
951
|
1180
|
1430
|
1680
|
1940
|
2240
|
2550
|
|
10.6
|
922
|
1140
|
1390
|
1640
|
1900
|
2190
|
2500
|
|
10.8
|
892
|
1110
|
1350
|
1600
|
1860
|
2150
|
2460
|
|
11.0
|
862
|
1070
|
1310
|
1560
|
1820
|
2110
|
2410
|
|
11.2
|
831
|
1040
|
1270
|
1510
|
1780
|
2070
|
2370
|
|
11.4
|
799
|
995
|
1220
|
1470
|
1730
|
2020
|
2320
|
|
11.6
|
763
|
953
|
1170
|
1410
|
1680
|
1970
|
2280
|
|
11.8
|
722
|
904
|
1120
|
1350
|
1620
|
1910
|
2230
|
|
12.0
|
641
|
807
|
1000
|
1220
|
1480
|
1790
|
2130
|
|
Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.
R = radius of curve Vd = design speed e = rate of superelevation
|
Source: A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission.
a different maximum superelevation rate. Table 2.7 shows values for a maximum rate of 0.04; Table 2.8, for 0.06; Table 2.9, for 0.08; Table 2.10, for 0.10; and Table 2.11, for 0.12. Method 5 was used to calculate the minimum radius for each superelevation rate less than the maximum rate in each design speed column in the tables.
The superelevation rates on low-speed urban streets are set using method 2 described above, in which side friction is used to offset the effect of centrifugal force up to the maximum friction value allowed for the design speed. Superelevation is then introduced for sharper curves. The design data in Table 2.12, based on method 2 and a maximum superelevation rate of 0.04, can be used for low-speed urban streets and temporary roads. The design data in Table 2.13 can be used for a wider range of design speeds and superelevation rates.
In attempting to apply the recommended superelevation rates for low-speed urban roadways, various factors may combine to make these rates impractical to obtain. These factors include wide pavements, adjacent development, drainage conditions, and frequent access points. In such cases, curves may be designed with reduced or no superelevation, although crown removal is the recommended minimum.
Effect of Grades on Superelevation. On long and fairly steep grades, drivers tend to travel somewhat slower in the upgrade direction and somewhat faster in the downgrade direction than on level roadways. In the case of divided highways, where each pavement can be superelevated independently, or on one-way roadways such as ramps, this tendency should be recognized to see whether some adjustment in the superelevation rate would be desirable and/or feasible. On grades of 4 percent or greater with a length of 1000 ft (305 m) or more and a superelevation rate of 0.06 or more, the designer may adjust the superelevation rate by assuming a design speed 5 mi/h (8 km/h) less in the upgrade direction and 5 mi/h (8 km/h) greater in the downgrade direction, provided that the assumed design speed is not less than the legal speed. On two-lane, two-way roadways and on other multilane undivided highways, such adjustments are less feasible, and should be disregarded.
Superelevation Methods. There are three basic methods for developing superelevation on a crowned pavement leading into and coming out of a horizontal curve. Figure 2.9 shows each method. In the most commonly used method, case I, the pavement edges are revolved about the centerline. Thus, the inner edge of the pavement is depressed by half of the superelevation and the outer edge raised by the same amount. Case II shows the pavement revolved about the inner or lower edge of pavement, and case III shows the pavement revolved about the outer or higher edge of pavement. Case II can be used where off-road drainage is a problem and lowering the inner pavement edge cannot be accommodated. The superelevation on divided roadways is achieved by revolving the pavements about the median pavement edge. In this way, the outside (high side) roadway uses case II, while the inside (low side) roadway uses case III. This helps control the amount of “distortion” in grading the median area.
Superelevation Transition. The length of highway needed to change from a normal crowned section to a fully superelevated section is referred to as the superelevation transition. This length is shown as X in Fig. 2.9, which also shows the various other elements described below. The superelevation transition is divided into two parts: the tangent runout, and the superelevation runoff.
The tangent runout (T in Fig. 2.9) is the length required to remove the adverse pavement cross slope. As is shown for case I of Fig. 2.9, this is the length required to raise the outside edge of pavement from a normal cross slope to a half-flat section. The superelevation runoff (L in Fig. 2.9) is the length required to raise the outside
TABLE 2.12 Superelevation Rates and Runoff Lengths (ft) for Horizontal Curves on Low-Speed Urban Streets Based on a Maximum Superelevation Rate of 4 Percent
Design speed, mi/h
20 25 30 35 40 45
Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.
Source: Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with
permission.
|
TABLE 2.13 Runoff Lengths (ft) for Horizontal Curves with Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 12 Percent Based on One Lane Rotated about the Centerline
|
e Vd
|
= 15 mi/h
|
Vd = 20 mi/h
|
Vd = 25 mi/h
|
Vd = 30 mi/h
|
Vd = 35 mi/h
|
II
О
3
|
Vd = 45 mi/h
|
|
(%)
|
L (ft)
|
L (ft)
|
L (ft)
|
Lr (ft)
|
L (ft)
|
Lr (ft)
|
L (ft)
|
|
1.5
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
2.0
|
31
|
32
|
34
|
36
|
39
|
41
|
44
|
|
2.2
|
34
|
36
|
38
|
40
|
43
|
46
|
49
|
|
2.4
|
37
|
39
|
41
|
44
|
46
|
50
|
53
|
|
2.6
|
40
|
42
|
45
|
47
|
50
|
54
|
58
|
|
2.8
|
43
|
45
|
48
|
51
|
54
|
58
|
62
|
|
3.0
|
46
|
49
|
51
|
55
|
58
|
62
|
67
|
|
3.2
|
49
|
52
|
55
|
58
|
62
|
66
|
71
|
|
3.4
|
52
|
55
|
58
|
62
|
66
|
70
|
76
|
|
3.6
|
55
|
58
|
62
|
65
|
70
|
74
|
80
|
|
3.8
|
58
|
62
|
65
|
69
|
74
|
79
|
84
|
|
4.0
|
62
|
65
|
69
|
73
|
77
|
83
|
89
|
|
4.2
|
65
|
68
|
72
|
76
|
81
|
87
|
93
|
|
4.4
|
68
|
71
|
75
|
80
|
85
|
91
|
98
|
|
4.6
|
71
|
75
|
79
|
84
|
89
|
95
|
102
|
|
4.8
|
74
|
78
|
82
|
87
|
93
|
99
|
107
|
|
5.0
|
77
|
81
|
86
|
91
|
97
|
103
|
111
|
|
5.2
|
80
|
84
|
89
|
95
|
101
|
108
|
116
|
|
5.4
|
83
|
88
|
93
|
98
|
105
|
112
|
120
|
|
5.6
|
86
|
91
|
96
|
102
|
108
|
116
|
124
|
|
5.8
|
89
|
94
|
99
|
105
|
112
|
120
|
129
|
|
6.0
|
92
|
97
|
103
|
109
|
116
|
124
|
133
|
|
6.2
|
95
|
101
|
106
|
113
|
120
|
128
|
138
|
|
6.4
|
98
|
104
|
110
|
116
|
124
|
132
|
142
|
|
6.6
|
102
|
107
|
113
|
120
|
128
|
137
|
147
|
|
6.8
|
105
|
110
|
117
|
124
|
132
|
141
|
151
|
|
7.0
|
108
|
114
|
120
|
127
|
135
|
145
|
156
|
|
7.2
|
111
|
117
|
123
|
131
|
139
|
149
|
160
|
|
7.4
|
114
|
120
|
127
|
135
|
143
|
153
|
164
|
|
7.6
|
117
|
123
|
130
|
138
|
147
|
157
|
169
|
|
7.8
|
120
|
126
|
134
|
142
|
151
|
161
|
173
|
|
8.0
|
123
|
130
|
137
|
145
|
155
|
166
|
178
|
|
8.2
|
126
|
133
|
141
|
149
|
159
|
170
|
182
|
|
8.4
|
129
|
136
|
144
|
153
|
163
|
174
|
187
|
|
8.6
|
132
|
139
|
147
|
156
|
166
|
178
|
191
|
|
8.8
|
135
|
143
|
151
|
160
|
170
|
182
|
196
|
|
9.0
|
138
|
146
|
154
|
164
|
174
|
186
|
200
|
|
9.2
|
142
|
149
|
158
|
167
|
178
|
190
|
204
|
|
9.4
|
145
|
152
|
161
|
171
|
182
|
194
|
209
|
|
9.6
|
148
|
156
|
165
|
175
|
186
|
199
|
213
|
|
9.8
|
151
|
159
|
168
|
178
|
190
|
203
|
218
|
|
10.0
|
154
|
162
|
171
|
182
|
194
|
207
|
222
|
|
10.2
|
157
|
165
|
175
|
185
|
197
|
211
|
227
|
|
10.4
|
160
|
169
|
178
|
189
|
201
|
215
|
231
|
|
10.6
|
163
|
172
|
182
|
193
|
205
|
219
|
236
|
|
10.8
|
166
|
175
|
185
|
196
|
209
|
223
|
240
|
|
11.0
|
169
|
178
|
189
|
200
|
213
|
228
|
244
|
|
11.2
|
172
|
182
|
192
|
204
|
217
|
232
|
249
|
|
11.4
|
175
|
185
|
195
|
207
|
221
|
236
|
253
|
|
11.6
|
178
|
188
|
199
|
211
|
225
|
240
|
258
|
|
11.8
|
182
|
191
|
202
|
215
|
228
|
244
|
262
|
|
12.0
|
185
|
195
|
206
|
218
|
232
|
248
|
267
|
(Continued)
|
|
TABLE 2.13 Runoff Lengths (ft) for Horizontal Curves with Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 12 Percent Based on One Lane Rotated about the Centerline (Continued)
|
e V
|
= 50 mi/h
|
Vd = 55 mi/h
|
Vd = 60 mi/h
|
Vd = 65 mi/h
|
Vd = 70 mi/h
|
Vd = 75 mi/h
|
Vd = 80 mi/h
|
|
(%)
|
Lr (ft)
|
Lr (ft)
|
Lr (ft)
|
Lr (ft)
|
Lr (ft)
|
Lr (ft)
|
Lr (ft)
|
|
1.5
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
2.0
|
48
|
51
|
53
|
56
|
60
|
63
|
69
|
|
2.2
|
53
|
56
|
59
|
61
|
66
|
69
|
75
|
|
2.4
|
58
|
61
|
64
|
67
|
72
|
76
|
82
|
|
2.6
|
62
|
66
|
69
|
73
|
78
|
82
|
89
|
|
2.8
|
67
|
71
|
75
|
78
|
84
|
88
|
96
|
|
3.0
|
72
|
77
|
80
|
84
|
90
|
95
|
103
|
|
3.2
|
77
|
82
|
85
|
89
|
96
|
101
|
110
|
|
3.4
|
82
|
87
|
91
|
95
|
102
|
107
|
117
|
|
3.6
|
86
|
92
|
96
|
100
|
108
|
114
|
123
|
|
3.8
|
91
|
97
|
101
|
106
|
114
|
120
|
130
|
|
4.0
|
96
|
102
|
107
|
112
|
120
|
126
|
137
|
|
4.2
|
101
|
107
|
112
|
117
|
126
|
133
|
144
|
|
4.4
|
106
|
112
|
117
|
123
|
132
|
139
|
151
|
|
4.6
|
110
|
117
|
123
|
128
|
138
|
145
|
158
|
|
4.8
|
115
|
123
|
128
|
134
|
144
|
152
|
165
|
|
5.0
|
120
|
128
|
133
|
140
|
150
|
158
|
171
|
|
5.2
|
125
|
133
|
139
|
145
|
156
|
164
|
178
|
|
5.4
|
130
|
138
|
144
|
151
|
162
|
171
|
185
|
|
5.6
|
134
|
143
|
149
|
156
|
168
|
177
|
192
|
|
5.8
|
139
|
148
|
155
|
162
|
174
|
183
|
199
|
|
6.0
|
144
|
153
|
160
|
167
|
180
|
189
|
206
|
|
6.2
|
149
|
158
|
165
|
173
|
186
|
196
|
213
|
|
6.4
|
154
|
163
|
171
|
179
|
192
|
202
|
219
|
|
6.6
|
158
|
169
|
176
|
184
|
198
|
208
|
226
|
|
6.8
|
163
|
174
|
181
|
190
|
204
|
215
|
233
|
|
7.0
|
168
|
179
|
187
|
195
|
210
|
221
|
240
|
|
7.2
|
173
|
184
|
192
|
201
|
216
|
227
|
247
|
|
7.4
|
178
|
189
|
197
|
207
|
222
|
234
|
254
|
|
7.6
|
182
|
194
|
203
|
212
|
228
|
240
|
261
|
|
7.8
|
187
|
199
|
208
|
218
|
234
|
246
|
267
|
|
8.0
|
192
|
204
|
213
|
223
|
240
|
253
|
274
|
|
8.2
|
197
|
209
|
219
|
229
|
246
|
259
|
281
|
|
8.4
|
202
|
214
|
224
|
234
|
252
|
265
|
288
|
|
8.6
|
206
|
220
|
229
|
240
|
258
|
272
|
295
|
|
8.8
|
211
|
225
|
235
|
246
|
264
|
278
|
302
|
|
9.0
|
216
|
230
|
240
|
251
|
270
|
284
|
309
|
|
9.2
|
221
|
235
|
245
|
257
|
276
|
291
|
315
|
|
9.4
|
226
|
240
|
251
|
262
|
282
|
297
|
322
|
|
9.6
|
230
|
245
|
256
|
268
|
288
|
303
|
329
|
|
9.8
|
235
|
250
|
261
|
273
|
294
|
309
|
336
|
|
10.0
|
240
|
255
|
267
|
279
|
300
|
316
|
343
|
|
10.2
|
245
|
260
|
272
|
285
|
306
|
322
|
350
|
|
10.4
|
250
|
266
|
277
|
290
|
312
|
328
|
357
|
|
10.6
|
254
|
271
|
283
|
296
|
318
|
335
|
363
|
|
10.8
|
259
|
276
|
288
|
301
|
324
|
341
|
370
|
|
11.0
|
264
|
281
|
293
|
307
|
330
|
347
|
377
|
|
11.2
|
269
|
286
|
299
|
313
|
336
|
354
|
384
|
|
11.4
|
274
|
291
|
304
|
318
|
342
|
360
|
391
|
|
11.6
|
278
|
296
|
309
|
324
|
348
|
366
|
398
|
|
11.8
|
283
|
301
|
315
|
329
|
354
|
373
|
405
|
|
12.07
|
288
|
306
|
320
|
335
|
360
|
379
|
411
|
Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.
Source: A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission.
|
NOTE: The diagrams below show positioning of the superelevation transition for both simple curves and spiral curves. Only one of these conditions would exist for a given transition.
LEGEND: X = Length of superelevation transition.
L = Length of superelevation runoff.
T = Tangent runout R = Crown removal
G = Equivalent slope rate of Change of outside pavement edge compared to the control line In each case. (See Table 2.13 for values.)
N = Normal cross slope S = Full superelevation rate
FIGURE 2.9 Superelevation transition between tangent and simple or spiral curves for three cases. (From Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with permission) edge of pavement from a half-flat section to a fully superelevated section. The length of transition required to remove the pavement crown (R in Fig. 2.9) is generally equal to twice the T distance.
The minimum superelevation transition length X should be equal in feet to 3 times the design speed in miles per hour. This includes the tangent runout (T) as previously described. The reason to specify this minimum is to avoid the appearance of a “kink” in
the roadway that a shorter transition would provide. The distance is approximately equal to that traveled by a vehicle in 2 s at design speed. This requirement does not apply to low-speed roadways, temporary roads, superelevation transitions near intersections, or transitions between adjacent horizontal curves (reverse or same direction) where normal transitions would overlap each other. In these cases, the minimum transition length is determined by multiplying the edge of pavement correction by the equivalent slope rate (G) shown in Table 2.14. The rate of change of superelevation should be constant throughout the transition X. Some agencies use a flatter rate of transition through the T or R sections than that recommended in Table 2.14, an acceptable but unnecessary practice.
The values given for Lr in Tables 2.12 and 2.13 are based on one 12-ft (3.66-m) lane revolved about the centerline. Table 2.14 shows methods of calculating L when more lanes are revolved about the centerline. In the equations in Table 2.14, L is substituted for Lr. In addition to the terms described in Fig. 2.9, two additional ones are used. W is the width from the point of revolution to the outside edge of pavement. For example, if three 12-ft (3.66-m) lanes are revolved about the lane edge between lanes 2 and 3, then W = 3 X 12 = 36 ft (11 m); the wider section of pavement is used for the width. B is an adjustment factor for multilane pavements to allow for some reduction in the superelevation transition for roads other than interstates, freeways, expressways, and ramps. Section (a) in Table 2.14 lists the equivalent slope rate values G for the various design speeds. Section (b) provides the multilane adjustments factors B for the speeds. Section (c) calculates the value of the overall transition length X based on the values given in (a) and (b) along with a given W and S for each case in Fig. 2.9. Finally, section (d) tests the values calculated to ensure that the minimum transition length discussed in this section is provided. Values for X, L, and T can be lengthened if necessary to achieve a 2-s transition time.
Superelevation Position. Figure 2.9 shows the recommended positioning of the proposed superelevation transition in relationship to the horizontal curve. For those curves with spirals, the transition from adverse crown removal to full superelevation should occur within the limits of the spiral. In other words, the spiral length should equal the L value, usually rounded to the nearest 25 ft (7.6 m).
For simple curves without spirals, the L transition should be placed so that 50 to 70 percent of the maximum superelevation rate is outside the curve limits (point of curvature PC to point of tangency PT). It is recommended that whenever possible, two-thirds of the full superelevation rate be present at the PC and PT. See the case diagrams in Fig. 2.9 for a graphic presentation of the recommended positioning.
Profiles and Elevations. Breakpoints at the beginning and end of the superelevation transition should be rounded to obtain a smooth profile. One suggestion is to use a “vertical curve” on the edge of the pavement profile with a length in feet equal to the design speed in mi/h (i. e., 45 ft for 45 mi/h). The final construction plans should have the superelevation tables or pavement details showing the proposed elevations at the centerline, pavement edges, and, if applicable, lane lines or other breaks in the cross slopes. Pavement or lane widths should be included where these widths are in transition. Pavement edge profiles should be plotted to an exaggerated vertical profile within the limits of the superelevation transitions to check calculations and to determine the location of drainage basins. Adjustments should be made to obtain smooth profiles. Special care should be taken in determining edge elevations in a transition area when the profile grade is on a vertical curve.
Superelevation between Reverse Horizontal Curves. When two horizontal curves are in close proximity to each other, the superelevation transitions calculated independently
|
TABLE 2.14 Superelevation Notes for Adjusting Runoff Lengths in Tables 2.12 and 2.13
(a) Maximum relative gradients for profiles between the edge of pavement and the centerline or reference line
|
Design speed, mi/h
|
Relative
gradient
|
Equivalent slope rate, G
|
|
20
|
0.74
|
135:1
|
|
25
|
0.70
|
143:1
|
|
30
|
0.66
|
152:1
|
|
35
|
0.62
|
161:1
|
|
40
|
0.58
|
172:1
|
|
45
|
0.54
|
185:1
|
|
50
|
0.50
|
200:1
|
|
55
|
0.47
|
213:1
|
|
60
|
0.45
|
222:1
|
|
65
|
0.43
|
233:1
|
|
70
|
0.40
|
250:1
|
|
|
(b) Transition length adjustment factors for wide pavements
|
Number of lanes
|
B for interstates, freeways,
|
B for
|
|
from point of rotation
|
expressways, and ramps
|
other roadways
|
|
1.0
|
1.00
|
1.00
|
|
1.5
|
1.00
|
0.83
|
|
2.0
|
1.00
|
0.75
|
|
2.5
|
1.00
|
0.70
|
|
3.0
|
1.00
|
0.67
|
|
3.5
|
1.00
|
0.64
|
|
(c) Calculate X, L, T
|
|
Case I
|
Cases II and III
|
|
|
X = BW(S + N)G
|
X = BWSG
|
|
|
L = BWSG
|
L = BW(S – N/2)G
|
|
|
T = BWNG
|
T = BW(N/2)G
|
|
(d) Check for 2-second minimum transition
|
(Note: D is the linear ft equivalent of the design speed in mi/h. For example, D = 60 ft for 60 mi/h)
If X > 3D, then the values for X, L, and T from section (c) are valid.
If X < 3D, then recalculate X, L, and T as follows:
|
Case I
|
Cases II and III
|
|
X = 3D
|
X = 3D
|
|
L = 3D[S/(N + S)]
|
L = 3D[(2S – N)/2S]
|
|
T = 3D[N/(N + S)]
|
T = 3D(N/2S)
|
Conversion: 1 mi/h = 1.609 km/h.
General notes:
1. The Lr in Tables 2.12 and 2.13 is the same as L in Table 2.14 and is based on a two-lane 24-ft pavement revolved about the centerline.
2. Adjustments to L for varying two-lane pavement widths can be made by direct proportion. For a 20-ft pavement revolved about the centerline, L’ = L(20/24).
3. Determination of X, L, and T when more than one lane is revolved about the centerline (or other reference line, such as a baseline or edge of pavement) is shown in part (c). Values for G and B in the formulas are given in parts (a) and (b), respectively. The value for W is the pavement width from the point of rotation to the farthest edge.
4. The minimum length of superelevation transition (X) as discussed in the text is the distance traveled in 2 s. This number can be rounded off to a figure in feet equal to 3 times the design speed. In part (d) the calculated X value is compared to the value of 3D, where D is the linear feet equivalent of the design speed in miles per hour. If the value of 3D is larger, X is set equal to this value and L and T are adjusted accordingly.
5. The L value is also the recommended spiral length where spirals are used.
Source: Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with
permission.
may overlap each other. In these cases, the designer should coordinate the transitions to provide a smooth and uniform change from the full superelevation of the first curve to the full superelevation of the second curve. Figure 2.10 shows two diagrams suggesting ways in which this may be accomplished. In both diagrams each curve has its own L value (L1, L2) depending on the degree of curvature, and the superelevation is revolved about the centerline.
|
PAV
|
‘EMENT REVOLVED ABC
LI
|
3UT THE CENTERLINE
L2
|
—
|
|
JL.
|
-50Lito. TOLi,
|
.50L2to. T0L2
|
—– .—————– —–
|
|
D.
|
|
|
|
—
|
PT«
|
|
® PCI
|
—_______ d)
2 ———————-
|
|
|
S.-5 Ut
SIMPLE CURVES
|
|
PA
|
VEMENT REVOLVED ABOUT THE CENTERLINE
. L3
|
—
|
|
LI
|
|
L2
|
|
D
|
|
|
|
|
|
|
|
CS«I
|
ST[1]I
|
|
TS
|
|
SC*2
|
|
SPIRAL CURVES
|
LEGEND:
(A) – Centerline Pavement (D – Outside EP. Curve I,
Inside EP. Curve 2 E. P.=Edge of Pavement
© – Inside EP, Curve I, Outside EP. Curve 2 Si, S2 = Superelevation Rates: Curves I & 2 Li, L2 = Superelevation Transition Lengths: Curves I <t 2 D = Distance between Curves
L3 = Total Superelevation Transition between Spiral Curves
FIGURE 2.10 Superelevation transition between reverse horizontal curves, simple or spiral. (From Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with permission)
The top diagram involves two simple curves. In the case of new or relocated alignment, the PT of the first curve and the PC of the second curve should be separated by enough distance to allow a smooth, continuous transition between the curves at a rate not exceeding the G value for the design speed (Table 2.14). This requires that the distance be not less than 50 percent nor greater than 70 percent of L1 + L2. Two-thirds is the recommended portion. When adapting this procedure to existing curves where no alignment revision is proposed, the transition should conform as closely as possible to the above criteria. When the available distance between the curves is less than 50 percent of L1 + L2, the transition rate may be increased and/or the superelevation rate at the PT or PC may be set to less than 50 percent of the full superelevation rate.
The lower diagram involves two spiral curves. Where spiral transitions are used, the spiral-to-tangent (ST) point of the first curve and the tangent-to-spiral (TS) transition of the second curve may be at, or nearly at, the same location, without causing superelevation problems. In these cases, the crown should not be reestablished as shown in Fig. 2.9, but instead, both pavement edges should be in continual transition between the curves, as shown in the lower diagram of Fig. 2.10. The total superelevation transition length is the distance between the curve-to-spiral (CS) point of the first curve and spiral-to-curve (SC) point of the second curve.
Spiral Transitions. When a motor vehicle enters or leaves a circular horizontal curve, it follows a transition path during which the driver makes adjustments in steering to account for the gain or loss in centrifugal force. For most curves, the average driver can negotiate this change in steering within the normal width of the travel lane. However, combinations of higher speeds and sharper curvature may cause the driver to move into an adjacent travel lane while accomplishing the change. To prevent this occurrence, the designer should use spirals to smooth out transitions.
There are several advantages to using spiral transitions for horizontal curves:
• They provide an easy-to-follow path for the driver to negotiate.
• They provide a convenient area in which to place the superelevation transition.
• They provide an area where the pavement width can be transitioned when required for curve widening.
• They provide a smoother appearance to the driver.
The Euler spiral is the one most commonly used in highway design. The degree of curve varies gradually from zero at the tangent end to the degree of the circular arc at the curve end. By definition, the degree of curve at any point along the spiral varies directly with the length measured along the spiral. In the case where a spiral transition connects two simple curves, the degree of curve varies directly from that of the first circular arc to that of the second circular arc. As a general guideline, spirals should be used on roadways where the design speed is 50 mi/h (80 km/h) or greater and the degree of curvature exceeds the values given in Table 2.15 for various design speeds listed.
Horizontal Alignment Considerations. The following items should be considered when establishing new horizontal alignment: •
|
TABLE 2.15 Maximum Curve without a Spiral
|
Design speed, mi/h
|
Design speed, km/h
|
Max. degree of curve
|
Min. radius, ft
|
Min. radius, m
|
|
50
|
80
|
4°30′
|
1273
|
388
|
|
55
|
88
|
3°45′
|
1528
|
466
|
|
60
|
96
|
3°00′
|
1910
|
582
|
|
65
|
105
|
2°30′
|
2292
|
699
|
|
70
|
113
|
2°15′
|
2546
|
776
|
Source: Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with permission.
|
• Tangents and/or flat curves should be provided on high, long fills.
• Compound curves should be used only with caution.
• Abrupt alignment reversals should be avoided.
• Two curves in the same direction separated by a short tangent (broken-back or flat – back curves) should be avoided.
![]()


![]()
![]()

 ing must have a minimum of five plies. Avoid three-ply, h-in. CDX. Although it is widely available and cheaper than five-ply, it’s vastly inferior.
ing must have a minimum of five plies. Avoid three-ply, h-in. CDX. Although it is widely available and cheaper than five-ply, it’s vastly inferior.





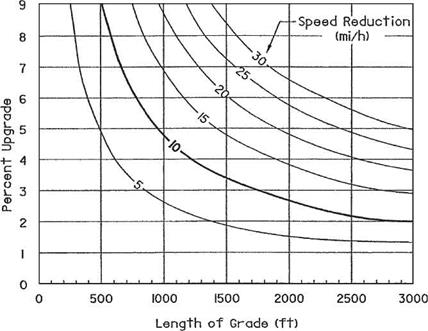
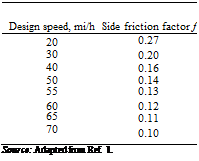

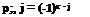 rfr + i (-1)r j (r + j )!
rfr + i (-1)r j (r + j )!![Statistical Properties of Random Variables Подпись: рЖ рЖ E {T [Ft (T )^}= / [t Ft (t)] ft (t) dt = [t(1 - e-t/0 )](e—t/0/0) dt = 40 00](/img/1312/image082_1.png) 01 =
01 =





 8×4 I-beam that’s 0.245 in. thick weighs roughly 300 lb.; whereas, a 20-ft., 8x8H I-beam with a web that’s 0.458 in. thick weighs 800 lb. If you order a nonstandard size, expect to pay a premium.
8×4 I-beam that’s 0.245 in. thick weighs roughly 300 lb.; whereas, a 20-ft., 8x8H I-beam with a web that’s 0.458 in. thick weighs 800 lb. If you order a nonstandard size, expect to pay a premium.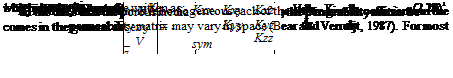
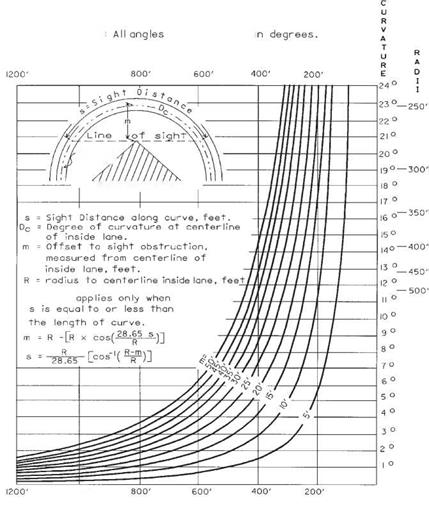 SIGHT DISTANCE
SIGHT DISTANCE

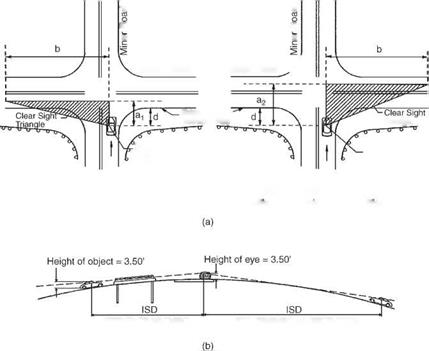 PORTION OF ABUTMENT
PORTION OF ABUTMENT
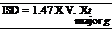
 Using S = intersection sight distance L = length of crest vertical curve A = algebraic difference in grades (%), absolute value K = rate of vertical curvature
Using S = intersection sight distance L = length of crest vertical curve A = algebraic difference in grades (%), absolute value K = rate of vertical curvature