Category WATER IN ROAD STRUCTURES

Broadly graded aggregates, as typically used in granular base and sub-base layers of the road construction have relatively small pores as the large pores between the coarser particles are mostly filled with smaller particles. This means that coefficient of permeability values, as characterised by the Darcy coefficient, K, are relatively low. Laboratory testing of typical sub-base aggregates has revealed hydraulic con­ductivity values that are usually less than 10-3 m/s in the unlikely even of saturation (Jones and Jones, 1989) and as low as an effective value of 10-6 m/s when, more normally, in a partially saturated state.

A second implication is that the pores will have a measurable suction ability. Hence dryer aggregates will usually show an ability to pull water towards them. There is a draft CEN standard (1999) for the evaluation of the suction height (i. e. of matric potential which is an indirect measure of the suction capacity of the aggre­gate). Figure 2.12 shows a result obtained by a similar method in which a column of

Measurement Techniques for Water Flow

SigurSur Erlingsson[4], Susanne Baltzer, Jose Baena and Gunnar Bjarnason

Abstract The chapter describes different measurement techniques for water-flow – related phenomena in pavements and embankments, i. e. water content, permeability and suction. For estimating the water content the gravimetric method is described as well as non-destructive methods such as neutron scattering, time domain reflectom – etry and ground penetrating radar. Then methods for estimating both the saturated and the unsaturated permeability of soils and granular materials are described. Both steady-state and unsteady methods are mentioned. Finally, common methods for measuring soil suction are briefly introduced.

Keywords Water flow ■ measurements ■ water content ■ permeability ■ suction

3.1 Introduction

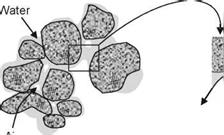
Water entering a pavement structure migrates as moisture through the structure. The amount of water penetrating the pavement is dependent on precipitation, drainage, design of the road structure, type and condition of the surface layer (cracks, joints) and shoulders and the materials in the pavement, subgrade and subsoil. Seasonal fluctuations in temperature, i. e. freezing and thawing, can also provoke moisture flow inside the pavement structure. An excess of water can cause a lower bear­ing capacity of the pavement structure and reduces pavement life (see Chapters 8 and 10). Also of concern is transport of contaminants with the liquid fluxes from the road and into the environment (see Chapter 6). As pavement deterioration can be reduced by proper drainage it is important to be able to measure the water content in order to understand how water moves within the road structure.

Predictions of water flow and contaminant transport in unsaturated soils should be based on an accurate description of the subsurface conditions including the aggregates

and hydrological properties of the materials involved. Therefore measurements of the fundamental parameters regarding flux of water need to be carried out. This also helps to set the initial conditions for analysis in water flow modelling.

The most important parameters related to the movement of water through pave­ment structures are the quantity and spatial distributions of moisture inside the pave­ment, the coefficient of permeability of individual layers and their matric suctions. These parameters can be determined experimentally, either in the field or in the laboratory, by various techniques. The most common of these methods used in road engineering will be briefly described in this chapter.

Water flow in unsaturated soils is primarily dependent on the volumetric water con­tent, matric suction and on the gravitational potential. Due to the presence of air within part of the pores, water movements are obstructed and flow is only achieved through the finer pores or in films around the soil particles. The permeability (or “hydraulic conductivity”) of unsaturated soils is, therefore, reduced compared with fully saturated soils due to the presence of air in the porous media. Usually the permeability of unsaturated soils is given as the water-relative permeability defined as the ratio of the permeability at a specific water content to its permeability under fully saturated conditions, thus:

K w (в)

krw (в) = – W (2.35)

K

where krw (в) is the water-relative permeability, Kw (в) is the water permeability – both being functions of the volumetric water content, в – while K is the saturated coefficient of permeability. Brooks and Corey (1964,1966) suggested that the water – relative permeability could be estimated as

krw (в) = 0V+ v (2.36)

where X is a the pore size distribution index and & is the normalized water content. Based on Mualem’s model (Mualem, 1976) van Genuchten (1980) expressed the water-relative permeability as:

Suction [cm] Vol. water content

Fig. 2.11 Water-relative permeability for a coarse (unbroken line) and fine grained (dotted line, mostly to the right in each figure) soil using van Genuchten’s equation. The parameters used to plot the curves are given in Table 2.2
where M is the same experimental parameter as given in the van Genuchten’s SWCC.

Figure 2.11 shows clearly that the permeability of a porous medium varies sig­nificantly with the suction or the volumetric water content (or degree of saturation as Sr = в/n). A reduction in the degree of saturation from fully saturated soil to 80% results in a relative permeability of only 36% of the saturated permeability for the sand and 18% for the clay respectively in the above figure. Hence, modelling water movements in pavement structures needs to address this to obtain a realistic movement of the water flow.

There is a number of parametric models that have been suggested in the literature for describing the matric potential’s dependency on water content (matric poten­tial being defined in Eq. 2.26). The models are all empirical and two frequently used are the power law model suggested by Brooks and Corey (1964) and the model suggested by van Genuchten (1980). For further details, see Fredlund and Rahardjo (1993), Fredlund and Xing (1994) and Apul et al. (2002).

The Brooks and Corey (1964) model is given as:

A

where the normalized water content, 0, is defined as:

The parameters вг and Srr are the irreducible (residual) volumetric water content and irreducible (residual) saturation respectively. The parameter Фь is the air entry value and the parameter A is called the pore size distribution index. The air entry value of the soil, Фь, is the matric suction at which air starts entering the largest pores in the soil (Fredlund et al., 1994). The parameter A characterizes the range of pores sizes within the soil, with larger values corresponding to a narrow size range and small values corresponding to a wide distribution of pore sizes.

The van Genuchten (1980) model relates the water content to the suction charac­teristics and is given as:

where a, N and M are experimentally determined parameters. Based on Mualem’s (1976) relative permeability model the parameters N and M are related as follows:

According to Fredlund and Xing (1994) this constraint between the parameters M and N reduces the flexibility of the van Genuchten model. They further claim that more accurate results can be achieved leaving the two parameters without any fixed relationship. Their model is a somewhat more general than the others and is based on the pore size distribution of the medium. It is given as:

M

where a, N and M are now different parameters to those of the van Genuchten model and also need to be estimated experimentally, but where n is the porosity and Ф is the matric potential in metres, as before (see Eq. 2.32). Figure 2.10 shows two typical soil water characteristic curves (SWCC) according to the van Genuchten model for coarse grained (unbroken line) and fine grained soils (dotted line) respec­tively. The parameters used for the two curves are given in Table 2.2.

Vol. water cont. Vol. water cont.

Fig. 2.10 Typical SWCC for a coarse (unbroken line) and fine grained (dotted line) soil using the van Genuchten’s model. The parameter used to plot the curves are given in Table 2.2

The soil water characteristic curve (SWCC) provides the relationship between the matric suction and water content for a given soil. In fact, calling the curve “character­istic” is something of a misnomer as the relationship is not solely a function of the soil type, but varies with (for example) temperature, pressure and pore water chemistry. A typical soil water characteristic curve for sand and clay can be seen in Fig. 2.9a.

Figure 2.9 shows clearly that, even at very high matric suctions (capillary pres­sures), all the water cannot be removed from the soil. The residual (or the irre­ducible) water content, usually denoted 0r (and in a similar way the irreducible water saturation, Srr) is the water content that is not removed in the soil even when a large amount of suction is applied.

Fig. 2.9 (a) Typical characteristic curves for coarse grained (gravel, sand) and fine grained soils (clay, silt). (b) Soil water characteristic curve showing drainage, wetting and scanning (intermedi­ate) curves. The dotted line represents the irreducible (residual) water content

1.5.1 Hysteresis Behaviour

For most soils the soil water characteristic curve (SWCC) shows hysteresis. This means that the 5 – в (or the Ф – 0) relationship depends on the saturation history
as well as on the existing water content. Figure 2.9b shows the SWCC for drainage and wetting conditions. The upper curve corresponds to a soil sample that is initially saturated and is drained by increasing the matric suction (capillary pressure), hence the drainage curve. The lower curve is called the wetting curve and gives the re­wetting of the soils with corresponding decrease in capillary pressure. If a wetting or a drainage process is stopped between the two endpoints and a reverse process is starting the scanning curves (indicated by arrows) are followed.

The groundwater table is defined as the locus of points at atmospheric pressure. Below the water table the pore water pressure is positive and in a hydrostatic state, while the pore water pressure increases linearly with depth. Above the groundwater table, in the vadose zone, water only remains in the pores due to capillary action. The water pressure is then negative or less than the atmospheric pressure and capillary pressures, known as matric suctions, exist. Large matric suctions correspond to large negative water phase pressures and soils under such conditions usually have low wa­ter saturations. Furthermore, both the water content and therefore the permeability are nonlinear functions of these capillary conditions.

In unsaturated soils, pore spaces are filled with both water and air. The water is held in the soil pores by surface tension forces. These lead to a pressure dif­ference between the air and water in the porous medium, as long as the interface is curved. As the curvature of the interface between the two phases – the air and the water – changes with the amount of water (or moisture content) in the soil, the matric suction is dependent on the water content. This relationship is non-linear, greatly complicating analyses of water flow through unsaturated soils.

The capillary conditions are described by the matric suction, 5 (expressed in pres­sure terms) or can be described in terms of the matric potential, Ф, which represents the height (head) of a column of water that could be induced by such a suction. Although negative with respect to zero (i. e. atmospheric pressure), Ф and 5 are usually expressed as positive quantities and are simply related as follows:

у

V = (2.26)

Pw g

where pw is the density of water and g is the acceleration due to gravity. Matric suction is related to the phase pressures and interface curvature by the relationship:

2оі

s = ua — u = – (2.27)

Гс

where ua and u are the air and water pressures, respectively, ai is the interfacial energy or the surface tension and rc is the average radii of curvature as illustrated in Fig. 2.8.

In the unsaturated zone, because part of the soil pores are filled with water while the rest is filled with air, therefore the sum of the volumetric water, в, and air, 9a, contents must be equal to the total porosity, n:

в + в a = П

This equation may also be written in terms of water saturation, Sr, that is

Sr + Sa = 1 (2.29)

where Sa is the air saturation content.

To understand the distribution of water in the unsaturated soils we may consider a soil mass that is initially dry. Upon addition of water, the water is first adsorbed as film on the surface of the soils grains. This thin skin of adsorbed water is usually called pellicular water (Bear, 1972) and is held strongly by van der Waal’s forces and can hold very high matric suctions. Thus even if a matric suction of tens of atmospheres were applied this water would not be removed from the soil.

If water is further added, water starts to accumulate at the contact point between the grains that represent the smallest pore space openings. This water is referred to as the pendular water. The pendular water is held at the contact points by capillary forces. Capillary forces are caused by the presence of surface tension between the air and the water phases within the soil voids and causes water to move into the

Fig. 2.8 (a) Distribution of water in a porous media. (b) Curved interface separating water and air phases

smallest pores. At this stage water movement through the soil skeleton is slow even under large hydraulic gradients because the water is forced to move along the thin film of adsorbed water. As the water content increases the film get thicker and water moves more easily.

As the water content continues to increase the water saturation reaches the stage where air becomes isolated in individual pockets in the larger pores and flow of air is no longer possible. This saturation is called insular saturation. These air pockets may dissolve leading to full water saturation of the soil.

Pavement structures consist of material layers with different grain size gradations and different mechanical as well as permeability properties. As water will flow through the structure it is important that migration of a portion of the fines from one layer to the next will not take place. To achieve this, the principles of fil – tration/separation must be applied at each interface (Cedergren, 1977). This is of special interest where water flows from fine grained material into a coarser grained material on its way out of the structure.

In applying the filter criteria the material to be drained is frequently referred to as the base material and the new material to be placed against it the filter material. The filter criteria stipulate that the filter needs to fulfil two functions:

• water needs to drain freely through it (filtration function or permeability criteria); and

• only a limited quantity of solid particles are allowed to move from the base layer into or through the filter layer (separation function or piping requirement). This criteria is set as otherwise the coarse grained material could be filled or clogged with time.

These two functions are in conflict with each other as filtration requires a high discharge through the filter while separation requires this to be small. The conditions of these two requirements can be expresses as:

—f —f

—5 > 4 to 5 & —5 < 4 to 5

D?5 — Ї5

where —15 is the diameter in the particle-size distribution curve for the filter material corresponding to 15% finer and — b5 and — b5 are the diameter in the particle-size distribution curve for the base material corresponding to 15% and 85% finer respec­tively. The application of these issues is presented in Chapter 13, Section 13.3.9.

Predicting the saturated permeability of soils or aggregates based on theoretical con­siderations has turned out to be difficult as permeability is dependent on a number of factors such as grading, void ratio, soil texture and structure, density and water tem­perature (Cedergren, 1977). Therefore, several empirical equations for estimating the permeability have been proposed in the past. These equations frequently include parameters linked to the grading curve of the material or their void ratio.

Hazen (1911) proposed an equation of the permeability of loose clean filter sand as:

K = cD2l0 (2.22)

where c is a constant that varies from 1.0 to 1.5 when the permeability K is in cm/s and the effective size D10 is in mm. Hazen’s equation is only valid for limited grain size distributions of sandy soils. A small quantity of silt or clay particles may change the permeability substantially. It is seldom a good means of estimating K as illustrated by Fig. 2.7.

Another form of equation that has been frequently used in estimating the perme­ability of sandy soils is based on the Kozeny-Carman equation (Das, 1997; Carrier, 2003):

10-

C

0)

и

« 10-4

Fig. 2.7 Illustration of mis-match between Hazen’s estimation and measured values from road aggregates (adapted from Jones and Jones, 1989) where c is a constant. Samarasinghe et al. (1982) proposed a similar equation for normally consolidated clays:

en

K = c (2.24)

1 + e

where n and c are experimentally determined parameters. These equations are al­most certainly improvements overEq. 2.22.

Water flows though porous media from a point to which a given amount of energy can be associated to another point at which the energy will be lower (Cedergren, 1974, 1977). The energy involved is the kinetic energy plus the potential energy. The kinetic energy depends on the fluid velocity but the potential energy is linked to the datum as well as the fluid pressure. As the water flows between the two points a certain head loss takes place.

From an experimental setup as shown in Fig. 2.6, the total energy of the system between points A and B is given from Bernoulli equation as

UA V A uB vB

— + TT + ZA = — + ^ + ZB + Ah Pwg 2g Pwg 2g

where u and v are the fluid pressure and velocity respectively, z is elevation above the datum line and h is head loss between point A and B that is generating the flow. As velocities are very small in porous media, velocity heads may be neglected, allowing head loss to be expressed as:

h = ^ + zA -( + zb) (2.14)

Pw g Pw g J

Darcy related flow rate to head loss per unit length through a proportion constant referred to as K, the coefficient of permeability (also known as the coefficient of hydraulic conductivity) as:

VK

P. S

p. g

B

Datum

Fig. 2.6 Head loss as water flows through a porous media. Where u = pore water pressures, h = heads, z & L = distances

or in more general terms, at an infinitesimal scale:

dh

v = -K = – Ki (2.16)

dl

where dh is the infinitesimal change in head over an infinitesimal distance, dl, and i is the hydraulic gradient of the flow in the flow direction. The above equation is known as Darcy’s law and governs the flow of water through soils (see Eq. 1.2).

It should be pointed out that Darcy’s law applies to laminar, irrotational flow of water in porous media. For saturated flow the coefficient of permeability may be treated as constant provided eddy losses are not significant (see below). Above the groundwater table, in the unsaturated zone, Darcy’s law is still valid but the permeability will be a function of the water content, thus K = K(9w), as described in Section 2.8.

Darcy’s law can easily be extended to two or three dimensions. For three dimen­sions using a Cartesian coordinate system Darcy’s law is given for a homogeneous isotropic medium as

highway engineering problems the porous media, that is each layer, can be assumed homogenous and isotropic.

For very coarse grained soils or aggregates, some of the voids in the material become quite large and the assumption of a laminar flow of water is no longer valid. Instead of irrotational flow, eddy currents develop in the larger voids and/or the flow may become turbulent involving more energy loss than in a laminar flow. For these circumstances the hydraulic gradient in Darcy’s law can be replaced with Forcheimer’s law:

, V V2

– = K + K

where two coefficient of permeability, K1 [LT-1] and K2 [L2T-2], are now required to describe the behaviour.

In highway practice this means that coarse aggregates with large pores – such as those which comprise typical granular base courses – must be tested at low hydraulic gradients to ensure laminar flow is maintained and that appropriate values of K are obtained. This aspect is covered further in Chapter 3, Section 3.3.1 (see Fig. 3.7 in particular).

Porosity is defined as the space inside a rock or sediment (soil), consisting of pores. The total volume of pores is defined as the total porosity. For water, only those pores that are interconnected are important. The interconnected part of the pore system is defined as the effective porosity. The porosity can be described as a three phase system comprising solids, water (liquid) and air (gas), see Fig. 2.5.

The definition of porosity, и, of an aggregate skeleton is the ratio of volume of voids and its bulk volume or:

n = V (m3/m3) (2.6)

Void ratio, e, is, on the other hand, defined as the ratio of the same volume of voids but now over its aggregate volume or:

The porosity represents the total amount in a unit volume that can be filled with wa­ter. The volumetric water content, в, is defined as the volume of water of a specific element to its total volume or:

в = Vw (m3/m3) (2.9)

and gives therefore the actual fraction of water in the pores. It is therefore obvious that the volumetric water content must lie within the range 0 < в < n.

The gravimetric water content, w (also referred to as the gravimetric moisture content), is on the other hand defined as the ratio of mass of water of an element to its mass of the solids or

mw

w = (kg/kg)

ms

Gravimetric water content is a much more commonly used measure than the volumetric water content. Therefore, unless stated otherwise or as required by the context, the gravimetric water content is indicated by the short form ‘water content’.

There is a simple relationship between the gravimetric water content, w, and the volumetric water content, в:

W mw m w ‘ g Pw ‘ Vw pw в

ms ms ■ g pd ■ V pd

where pw is the water density, pd is the dry density of the material and g is the acceleration due to gravity. The degree of water saturation is the volume of water per volume of void space, or:

The saturation range becomes, therefore 0 < Sr < 1 (100%).

Porosity of a geological material can change with time. According to their origins two types of porosity can be recognized, that is a primary and secondary porosity. The primary porosity refers to the original porosity of the material where the sec­ondary porosity refers to the portion of the total porosity resulting from diagenetic processes such as dissolution, post compaction, cementation or grain breakage.

Roads and embankments are made up by a finite number of layers. They can be considered as porous media that consist of aggregates or granular materials and soils through which fluid can flow. The road layer can appear either unbound or stabilized with bitumen or cement to increase their strength. In roads, most surface layers have very low permeability properties and can often be treated as impervious, at least in roads in good conditions. Usually, all others layers are permeable. The fluid flow behaviour of the different layers is strongly dependent on their particle size distribution and pore space openings.

2.4.1 Grain Size Distribution

The grain size distribution of unbound aggregates or soils is determined by either sieving or by the rate of settlement in an aqueous suspension. Table 2.1 shows the classification of soil particles or aggregates by size according to EN ISO 14688­1 (CEN, 2002). The distribution of coarse and very coarse soil fractions can be estimated through sieving but the size distribution of the fine soil particles needs to be estimated in a settlement rate test (hydrometer test).

Based on the grain size distribution curve three parameters are frequently deter­mined, that is the effective size D10, the uniformity coefficient Cu and coefficient of gradation Cc. The parameter D10 is the diameter of the largest particle that can be found in the smallest 10% of the particle-size distribution curve. The uniformity coefficient Cu and coefficient of gradation Cc are given as:

where D30 and D60 are the diameter on the particle-size distribution curve, similar to D10 but corresponding to 30% and 60% finest fractions respectively. These three parameters are sometimes used to estimate the saturated coefficient of permeability of some types of soils.