Category WATER IN ROAD STRUCTURES

Radiation is a process by which energy moves through a medium or vacuum without the movement of any molecules and without heating any medium through which it passes. The quantity of energy radiated from a grain surface increases with increased surface temperature and neighbouring grains increase their temperature by absorb­ing the radiation emitted. Because the higher-temperature grains radiate more en­ergy, radiation results in a net transfer of energy to the lower-temperature grains. For coarse dry soils heat conduction is low and 10-20% of heat transfer can be due to radiation. Generally though, radiation plays a negligible role for heat transfer in soils.

4.2.2 Vapour Diffusion

Vapour moves towards a lower vapour pressure by a molecular process known as diffusion (fundamentally the same process that redistributes contaminants in static water as described in Chapter 6, Section 6.3.1.). There is no need for there to be a conventional pressure differential, only a difference in the concentration of the vapour. Vapour pressure decreases with decreasing temperature and with decreasing relative humidity. That is, cold and dry areas attract vapour. Typically, at micro­scale, water evaporates at the warm end of a pore and condenses at the cold end, thereby transferring latent heat from the warm to the cold end of the pore.

4.2.3 Convection

Convection is energy transfer by macroscopic motion of fluid (liquid and gas) parti­cles. The fluid motion is the result of a force. The force may be due to a density gradient or due to a pressure difference generated by, for example, a pump, by gravity or induced differences of density. The moving particles bring their high or low energy with them. In soils, typically, the moving particles which transport heat are water molecules. Density gradients may be due to a gradient of water or of salt content. Because the density of water varies with temperature, the density gradient may be due to temperature gradient only.

The basic principles to model the complete time-dependent heat transfer in soils are described in this section. More details of these and the associated effects can be

found in some of the better or more specialist geotechnical textbooks, for example Mitchell and Soga (2005) or Fredlund and Rahardjo (1993).

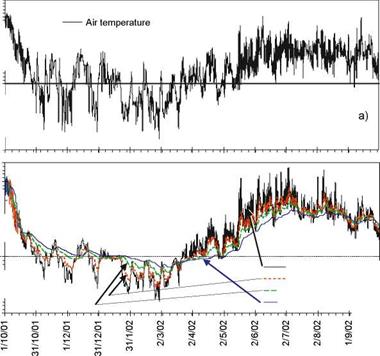
The water content in various road structures and the underlying soil are subject to climatic (temperature) effects. An example of the thermal variation in a road structure is given in Fig. 4.1. It can be clearly seen that the thermal state is definitely changing, which means that it is characterised by the heat transfer properties of the material. Temperatures may be positive or negative (inducing freezing). Heat trans­fer in soils is due to conduction, radiation, convection and vapour diffusion. A gen­eral overview of thermal transfer may be found in many textbooks, e. g. Selvadurai (2000) or Lewis and Schrefler (1998).

As pavement surface temperature depends greatly on the weather, typically changing hourly and daily, the physical process never reaches a steady state (i. e. there would be only a long-term equilibrium).

Geostructures, like road pavements and embankments, are made up of porous materials with solid and fluid phases. At micro-scale, i. e. the grains and pores scale, the heat transfer is highly complex, involving convection and radiation in the pores

25

20

15

10

-10

-15

-20

25

20

15

10

5

0

-5

-10

-15

and conduction in the grains. At the engineering scale (i. e. at macro-scale, at the layers thickness scale), the solid, liquid and gas phases may be considered separately as a continuum.

As discussed by Selvadurai (2000), it is known by experience that heat flows from points of higher temperature to points of lower temperature. Heat is, therefore, a form of energy, which is released by warmer regions of a body to the cooler regions.

Although heat flow cannot be measured directly, its presence manifests itself in terms of a measurable scalar quantity, which is the temperature. From the knowledge of the temperature distribution T(x, t) within a region, it is possible to calculate the heat flow within the region. As a consequence, the major part of the study of heat transfer in geostructures focuses on the determination of the temperature distribution within the medium which is subjected to appropriate boundary conditions and initial conditions applicable to T (x, t).

4.2.1 Conduction

Conduction refers to the mode of heat transfer where this energy transport takes place in the solid phase of the porous media and fluids, which are at rest. This is in contrast to convective heat transfer, which involves motion of a conducting fluid.

The grains of a soil, typically, are in contact with each other at distinct contact points and pores between grains are filled with a mixture of air and water. When completely dry the heat flow passes mainly through the grains, but has to bridge the air-filled gaps around the contact points. At very low water contents, thin adsorbed water layers cover the grains. The thickness of these layers increases with increasing water content as introduced in Chapter 2. At higher water contents, rings of liquid water form around the contact points between the grains. From this point on, the thermal conductivity increases rapidly with increasing water content. At even higher water contents, complete pores are filled with water resulting in a further but slower increase in thermal conductivity.

For a conducting medium which possesses homogeneity and isotropy with re­spect to its heat conduction characteristics (all parameters which govern the heat conduction process are assumed to be independent of direction and position), it is assumed that the amount of heat crossing an element of material in a given time, At, is proportional to the difference in temperature, T, and related to the material properties. Generalizing this concept leads to Fourier’s equation that defines a vector of heat flow Q (W/m2):

Q = – XV T = – XgradT (4.1)

where X(W/m°C) is defined as the thermal conductivity of the medium (see Section 4.3). Normally, the thermal conductivity of grains is in the range of 1-3 W/m°C. Water has a thermal conductivity of about 0.6 W/m°C at room tem­perature. In comparison with solids and liquids, the thermal conductivity of air is very small, being about 0.025 W/m°C.

For anisotropic materials like soils, Eq. 4.1 is generalized in matrix form:

Q = – A. V T = – XgradT

where X is the matrix of thermal conductivities.

Ake Hermansson[6], Robert Charlier, Frederic Collin, SigurSur Erlingsson, Lyesse Laloui and Mate Srsen

Abstract Temperature highly affects pavement performance. High and low tem­peratures not only affects the viscosity of asphalt concrete but also has an impact on the moisture flow within pavements. At temperatures below 0°C the freezing of pavements dramatically changes the permeability and frost action might occur forcing water to flow upwards to the freezing front resulting in frost heave and other pavement distress.

Keywords Heat transfer ■ conduction ■ temperature ■ frost

4.1 Introduction

The thermal state may have a major influence on the moisture condition of a pave­ment or foundation. Thermal gradients due to temperature changes on the surface will induce not only heat flow in the pavement but also moisture flow.

Freezing and thawing are definitely the most important aspects linking temper­ature to water flow. Furthermore, a freezing temperature significantly reduces the permeability of soils but also increases the moisture flow caused by hydraulic gra­dients due to ice lens formation in the frozen soil.

Moreover, the water viscosity depends on the temperature; at higher tempera­ture, some water will flow in the vapour phase, and this depends on the temperature gradient. Heat flow and moisture flow are, therefore, linked processes with complex interaction between them. This chapter will describe the basis of heat transfer laws and models.

Although far less common than in the laboratory, techniques for in-situ matric suc­tion measurements using the contact filter paper (CFP) method and in-situ total suction measurements using the non-contact filter paper method have also been described (Greacen et al., 1989). The filter paper technique is, in theory, applicable over the entire range of total suction, but the method tends to be impractical for both extremely high and extremely low suction values. Reliable measurements tend to be limited to a range spanning about 0-10 MPa matric suction for the contact filter paper techniques and between 1 to 10 MPa of total suction for the non-contact technique.

The filter paper method is used as an indirect means of measuring soil suction. The advantages of the method include its simplicity, its low cost, and its ability to measure a wide range of suction. Although this technique is more often used in the laboratory, the filter paper method has also been used in the field to measure soil suction. The CFP technique relies on measuring the equilibrium water content of small filter papers in direct contact with unsaturated soil specimens. Figure 3.17 shows the filter paper setup and installation to put it in direct contact with the soil specimen. In the laboratory the filter paper is placed in contact with the soil specimen in an airtight container for seven days and thereafter the water content of the filter paper is determined and the matric suction of the soil specimen is in­ferred from a calibration curve. Filter paper not in contact with the specimen permits water exchange only in the vapour phase and therefore measures the total suction (Rahardjo & Leong, 2006).

The water content of the filter paper at equilibrium is measured gravimetrically and related to matric soil suction through a predetermined calibration curve for the particular type of paper used. Commonly used types of papers include Whatman No. 42 and Schleicher and Schuell No. 589. Calibration and test procedures for the measurement of matric suction using the contact filter paper technique are described in the ASTM Standard D5298-94 (1997). However, different researchers have sug­gested different calibration curves for the same filter paper (Leong et al., 2002; Rahardjo and Leong, 2006).

3.2 Conclusions

A considerable variety of test and assessment procedures are available for measuring the volumetric and gravimetric water contents of both laboratory and in-situ road construction and geotechnical materials. The simplest tests to perform are usually destructive, but sophisticated geo-physical techniques are becoming increasingly common and usable, not only as identification tools, but also as quantitative mea­surement techniques.

Suction, which has such a large effect on the mechanical properties of soils and aggregates, is probably the quantity most difficult to measure successfully and must usually be monitored indirectly by the response of, e. g., water content and vapour monitoring. As the relationships between these secondary responses and the primary cause, suction, may both be imprecisely described and hysteretic there is usually some uncertainty in value of suction determined.

Permeability, another major quantity that needs evaluating, is more readily mea­sured using flow tests, but difficulties arise when measuring coarse-grained materi­als, such as road aggregates. Producing samples that are representative with respect to density and grading can be a challenge and the devices available for testing can allow water to preferentially flow along the edges, introducing further uncertainties into the assessment.

Nevertheless, a knowledge of permeability, suction and water content is indis­pensable for effective design and assessment of the movement of water in the high­way and its adjacent environment.

A simple laboratory variant of the tensiometer method for measuring matric suction of fine-grained soils uses a semi-pervious sintered glass plate. A small soil sample

is placed on the glass plate and covered immediately with a cap so that the vapour pressure around the soil comes to equilibrium with the suction in the soil, preventing drying. On the other side of the plate de-aired water is provided in a small chamber. The soil attempts to suck water across the glass plate from the chamber but the only way this can happen is by water being drawn into the chamber via a narrow-bore tube. In the tube, beyond the water, there is a small length of mercury and beyond that, air and a small hand-operated suction pump and vacuum gauge (Fig. 3.16). As the water (and, hence, the mercury) is pulled towards the soil, the operator applies a partial vacuum to oppose this and to keep the mercury in the same po­sition. Once the operator no longer needs to apply additional suction, the suction in the soil specimen and applied by the operator are in equilibrium and the suc­tion value may be read from the gauge. Typically, readings may be obtained in around 15 min (though this depends a lot on the soil type). The device is limited to measuring in the range from atmospheric pressure to approximately 70 kPa of suction.

Thermal conductivity sensors (TCS) are used to indirectly relate matric suction to the thermal conductivity of a porous medium embedded in a mass of unsaturated soil. Any change in the soil suction results in a corresponding change in the water content of the porous medium (governed by its characteristic curve). The thermal conductivity of a rigid porous medium is a direct function of the water content. Therefore, if the thermal conductivity of the porous medium is measured, the matric suction of the soil may be indirectly determined by correlation with a predetermined calibration curve. Figure 3.14 shows the main components of a modern commercial TCS.

Some disadvantages usually imputed to the old-fashioned TCS included the prob­lems associated with drift, and, for many sensors, deterioration in the sensor body over time, as well as uncertainties concerning the drying and rewetting processes due to hysteretic effects in the sensor calibration. But most of these problems have been resolved. The major advantages of the more recent TCS include the relative ease with which the sensors may be set up for automated data acquisition, their relatively low cost and their present capability to measure matric suction over a wide range (0-1200 kPa). Figure 3.15 shows some laboratory soil suction measure­ments carried out with both tensiometers and TCS, where tensiometer failures due to cavitation were noticeable. For further details regarding TCS see Rahardjo & Leong (2006).

One of the most common devices for measuring suction is a tensiometer. A ten­siometer consists of a fine porous ceramic cup connected by a tube to a vacuum

gauge (see Fig. 3.13). The entire device is filled with de-aired water. The porous tip is placed in intimate contact with the soil and the water flows through the porous cup (in or out) until the pressure inside the ceramic cup is in equilibrium with the pore water in the soil. The reading on the pressure measuring device, once corrected for the water column in the device, is the matric suction (Apul et al., 2002). The water pressure that can be measured by this method is limited to approximately -90 kPa, otherwise water will begin to boil inside the tensiometer (“cavitation”). Tensiome­ters have been found to provide the best measuring technique for low-range suction as they measure the pore pressures directly and respond promptly to pore water pressure changes (Rahardjo & Leong, 2006).

Lately, “high-capacity” tensiometers have been developed (e. g. Ridley & Burland, 1993; Guan& Fredlund, 1997; Tarantino andMongiovi, 2001). Whencou – pled with specialised operating procedures, for example, cyclic prepressurization techniques, they have been shown to be applicable for matric suction up to 1500 kPa. Comparisons with established measurement systems have shown high-capacity ten­siometers to be relatively reliable and quite rapid in terms of response time.

Soil suction or capillary pressure head can be measured either in the laboratory in an undisturbed sample of soil or directly in the field. Soil suction or total suc­tion consists of the matric suction and the osmotic suction. Their magnitudes can range from 0 to 1 GPa (Rahardjo & Leong, 2006). Today no single instrument or technique exists that can measure the entire range with reasonable accuracy. Suction measurement instruments can only measure suction up to about 10 MPa. In the highway environment soil suction in the low range (0-100 kPa) or the mid range (100kPa-1 MPa) is of most concern. There are different measurement tech­niques depending on which component of suction one wants to measure, matric or total. Usually in geotechnical engineering it is the matric suction that is measured. Table 3.2 summarises techniques for measuring suction in terms of approximate measuring range and applicability in the laboratory or field (Lu & Likos, 2004; Rahardjo & Leong, 2006). As it is generally not necessary to take osmotic suc­tion into account in routine geotechnical engineering practice, only the main in-situ methods for measuring matric suction are referred to. They include tensiometers, thermal conductivity sensors and contact filter paper techniques.

Direct measurement of suction in aggregates is more difficult than in finer grained soils as it is difficult to establish an effective contact between the measuring de­vice and the pore space in the aggregates. In aggregates with a high proportion of fines, this may be achievable. Alternatively, indirect measures such as discussed in Chapter 2, Section 2.9, can be employed.

As introduced in Chapter 2, the flow of water in saturated soils is commonly de­scribed using Darcy’s law which relates the rate of water flow to the hydraulic gra­dient (Eq. 2.16). Furthermore the coefficient of permeability is relatively constant for a specific soil. Darcy’s law applies also to the flow of water through unsaturated soils. However the permeability of unsaturated soils can not be assumed generally to be constant (Richards, 1931; Fredlund & Rahardjo, 1993; Fredlund 1997). Per­meability now becomes predominantly a function of either the water content or the matric suction (see Chapter 2, Section 2.8). The main reason for this is linked to the fact that the pores in the material are the channels through which the wa­ter flows. In saturated soils all pores are filled with water, allowing the water to move. In unsaturated soils however not all the pores are filled with water. The air-filled pores are therefore not active in transporting water through the material. They can therefore be assumed to behave in a similar way as the solid phase. The permeability of unsaturated soils is therefore lower than in the same soil in a saturated state and decreases as the water content decreases or matric suction increases.

A number of methods exist to measure the unsaturated permeability of soils, both in the laboratory and in the field. As for saturated methods, they can be classified into steady or unsteady methods. In the laboratory the steady state method is rec­ommended as it is relatively simple and has few ambiguities. However the method can be quite time consuming as the flow rate can be very low, especially under conditions of high matric suction. Further it can be difficult to measure the low flow rate accurately due to air diffusion. More recently a faster steady state method has been introduced where a centrifuge is introduced to drive the fluid flow (Nimmo et al., 1987; 1992). The unsteady laboratory methods, such as the thermal method, instantaneous profile method and the multi-step outflow method are usually much quicker than the traditional steady state method but are usually not as accurate. In the field the tension infiltrometer, instantaneous profile method and the cone penetrom­eter methods can be used. Benson & Gribb (1997) give a comprehensive overview of methods to measure the permeability of unsaturated soils.

The coefficient of permeability of unsaturated soils is not routinely measured in the laboratory as the process is cumbersome and quite time consuming (Fredlund 2006). The permeability of unsaturated soils can also be indirectly estimated from the SWCC. This is attractive as the SWCC can be determined in a much shorter time than the permeability’s dependency on matric suction and with greater reliability (Rahardjo & Leong, 1997).

In the steady state method, the unsaturated permeability is measured under con­ditions of a constant matric suction. A constant hydraulic head gradient is applied over an unsaturated soil sample with a constant matric suction to produce a steady state water flow through the specimen (see Fig. 3.11). A Mariotte bottle can be used to provide a constant pore water pressure to deliver a constant rate of flow. When the rates of water flow entering and leaving the sample are equal, the steady state has been reached and the coefficient of the permeability can be calculated according to Darcy’s law (Eq. 2.15) as

h u і — u2

v = – K – = K— 2 (3.14)

L pwgL

where v is the flow rate of water through the sample, K is the coefficient of perme­ability and h/L is the hydraulic head gradient across the sample (with h the head difference and L the length of the sample). The head difference can be estimated from ui and u2, the readings from the two pore water pressure sensors, converting pressure to head by dividing by the density of water, pw and the acceleration due to gravity, g.

Now the test is repeated for different suctions in order to establish the relationship between the permeability and the suction. A typical measurement of permeability as a function of the matric suction is given in Fig. 3.12. As matric suction is related to water content through the SWCC, and if that relationship is known, the variation of permeability with water content is also known. Notice that, for the suction range illustrated, the coefficient of permeability changes by 6 orders of magnitude.

Tracer tests involve the injection of an inert solution, or tracer, into an existing flow field via a borehole or a well. Tracer tests are often desirable because they are passive-type tests and do not place unnatural stress conditions on the flow system.

The dilution rate of the tracer at the injection well or its time of travel to another well can be used to calculate the water velocity and ultimately the permeability. Detection of the tracer, or concentration measurements, can be made by either manual or probe sampling. Commonly used tracers are radioisotopes, salt solutions and fluorescent dyes.