Category HIGHWAY ENGINEERING HANDBOOK

Horizontal Alignment and Superelevation

Posted by admin on 12/ 11/ 15

The horizontal alignment of a roadway should be designed to provide motorists with a facility for driving in a safe and comfortable manner. Adequate stopping sight distance should be furnished. Also, changes in direction should be accompanied by the use of curves and superelevation when appropriate in accordance with established guidelines. Some changes in alignment are slight and may not require curvature. Table 2.5 lists the maximum deflection angle which may be permitted without the use of a horizontal curve for each design speed shown. It is assumed that a motorist can easily negotiate the change in direction and maintain control over the vehicle without leaving the lane.

TABLE 2.4 Decision Sight Distance (DSD) for Design Speeds from 30 to 70 mi/h (48 to 113 km/h)

Decision sight distance, ft
Avoidance maneuver

Design speed, mi/h	A	B	C	D	E
30	220	490	450	535	620
35	275	590	525	625	720
40	330	690	600	715	825
45	395	800	675	800	930
50	465	910	750	890	1030
55	535	1030	865	980	1135
60	610	1150	990	1125	1280
65	695	1275	1050	1220	1365
70	780	1410	1105	1275	1445

• The avoidance maneuvers are as follows: A—rural stop; B—urban stop; C—rural speed/path/direction change; D—suburban speed/path/direction change; E—urban speed/path/direction change

• Decision sight distance (DSD) is calculated or measured using the same criteria as stopping sight distance: 3.50 ft (1.07 m) eye height and 2.00 ft (0.61 m) object height.

Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.

Source: Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of

Transportation, with permission.

TABLE 2.5 Maximum Centerline Deflection Not Requiring a Horizontal Curve

Design speed, mi/h Maximum deflection*

25	5°30′
30	3°45′
35	2°45′
40	2°15′
45	1°45′
50	1°15′
55	1°00′
60	1°00′
65	0°45′
70	0°45′
Based on the following formulas: Design speed 50 mi/h or over: tan A = 1.0/V Design speed under 50 mi/h: tan A = 60/V2

where V = design speed, mi/h A = deflection angle

Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.

Note: The recommended minimum distance between consecutive horizontal deflections is:

200 ft where design speed > 45 mi/h 100 ft where design speed < 45 mi/h *Rounded to nearest 15 min.

Source: Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with permission.

When centerline deflections exceed the values in Table 2.5, it is necessary to introduce a horizontal curve to assist the driver. Curves are usually accompanied by superelevation, which is a banking of the roadway to help counteract the effect of centrifugal force on the vehicle as it moves through the curve. In addition to superelevation, centrifugal force is also offset by the side friction developed between the tires of the vehicle and the pavement surface. The relationship of the two factors when considering curvature for a particular design speed is expressed by the following equation:

U. S. units: e + f =

V2 15V

(2.1a)

SI units: e + f =

127R

(2.1b)

where e = superelevation rate, ft per ft (m per m) of pavement width f = side friction factor V = design speed, mi/h (km/h)

R = radius of curve, ft (m)

In developing superelevation guidelines for use in designing roadways, it is necessary to establish practical limits for both superelevation and side friction factors. Several factors affect the selection of a maximum superelevation rate for a given highway. Climate must be considered. Regions subject to snow and ice should not be superelevated too sharply, because the presence of these adverse conditions causes motorists to drive slower, and side friction is greatly reduced. Consequently, vehicles tend to slide to the low side of the roadway. Terrain conditions are another factor. Flat areas tend to have relatively flat grades, and such conditions have little effect on superelevation and side friction factors. However, mountainous regions have steeper grades, which combine with superelevation rates to produce steeper cross slopes on the pavement than may be apparent to the designer. Rural and urban areas require different maximum superelevation rates, because urban areas are more frequently subjected to congestion and slower-moving traffic. Vehicles operating at significantly less than design speeds necessitate a flatter maximum rate. Given the above considerations, a range of maximum values has been adopted for use in design. A maximum rate of 0.12 or 0.10 may be used in flat areas not subject to ice or snow. Rural areas where these conditions exist usually have a maximum rate of 0.08. A maximum rate of 0.06 is recommended for urban high-speed roadways, 50 mi/h (80 km/h) or greater, while 0.04 is used on low-speed urban roadways and temporary roads.

Various factors affect the side friction factors used in design. Among these are pavement texture, weather conditions, and tire condition. The upper limit of the side friction factor is when the tires begin to skid. Highway curves must be designed to avoid skidding conditions with a margin of safety. Side friction factors also vary with design speed. Higher speeds tend to have lower side friction factors. The result of various studies leads to the values listed in Table 2.6, which shows the side friction factors by design speed generally used in developing superelevation tables (Ref. 1).

Taking into account the above limits on superelevation rates and side friction factors, and rewriting Eq. (2.1), it follows that for a given design speed and maximum superelevation rate, there exists a minimum radius of curvature that should be allowed for design purposes:

R. = ————— (2.2)

mn 15(e + f) v ‘

To allow a lesser radius for the design speed would require the superelevation rate or the friction factor to be increased beyond the recommended limit.

Подпись: Design speed, mi/h Side friction factor f 20 0.27 30 0.20 40 0.16 50 0.14 55 0.13 60 0.12 65 0.11 70 0.10 Source: Adapted from Ref. 1.

Highway design using U. S. Customary units defines horizontal curvature in terms of degree of curve as well as radius. Under this definition, the degree of curve is defined as the central angle of a 100-ft (30-m) arc using a fixed radius. This results in the following equation relating R (radius, ft) to D (degree of curve, degrees):

Подпись: (2.3) 5729.6

Substituting in Eq. (2.2) gives the maximum degree of curvature for a given design speed and maximum superelevation rate:

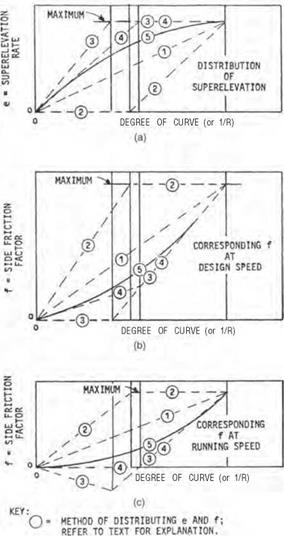
Before presenting the superelevation tables, one final consideration must be addressed. Because for any curve, superelevation and side friction combine to offset the effects of centrifugal force, the question arises how much superelevation should be provided for curves flatter than the “maximum” allowed for a given design speed. The following five methods have been used over the years (Ref. 1):

Method 1. Superelevation and side friction are directly proportional to the degree of curve or the inverse of the radius.

Method 2. Side friction is used to offset centrifugal force in direct proportion to the degree of curve, for curves up to the point where fmax is required. For sharper curves, fmax remains constant and e is increased in direct proportion to the increasing degree of curvature until e is reached.

Method 3. Superelevation is used to offset centrifugal force in direct proportion to the degree of curve for curves up to the point where emax is required. For sharper curves, emax remains constant and f is increased in direct proportion to the increasing degree of curvature until f is reached.

Method 4. Method 4 is similar to method 3, except that it is based on average running speed instead of design speed.

Method 5. Superelevation and side friction are in a curvilinear relationship with the degree of curve (inverse of radius), with resulting values between those of method 1 and method 3.

Figure 2.8 shows a graphic comparison of the various methods. Method 5 is most commonly used on rural and high-speed [50 mi/h (80 km/h) or higher] urban highways. Method 2 is used on low-speed urban streets and temporary roadways.

Recommended minimum radii for a given range of design speeds and incremental superelevation rates are given in Tables 2.7 through 2.11, where each table represents

Horizontal Alignment and Superelevation

FIGURE 2.8 Methods of distributing superelevation and side friction. (a) Superelevation. (b) Corresponding friction factor at design speed. (c) Corresponding friction factor at running speed. (From A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission)

TABLE 2.7 Minimum Radii for Design Speeds from 15 to 60 mi/ti (24 to 97 km/h) and Superelevation Rates to 4 Percent

e (%)	V, = 15 mi/h a R (ft)	V. = 20 mi/h a R (ft)	V, = 25 mi/h a R (ft)	V, = 30 mi/h a R (ft)	V. = 35 mi/h a R (ft)	V. = 40 mi/h a Я (ft)	V. = 45 mi/h a R (ft)	V, = 50 mi/h a R (ft)	V. = 55 mi/h a R (ft)	V. = 60 mi/h a R (ft)
1.5	796	1410	2050	2830	3730	4770	5930	7220	8650	10300
2.0	506	902	1340	1880	2490	3220	4040	4940	5950	7080
2.2	399	723	1110	1580	2120	2760	3480	4280	5180	6190
2.4	271	513	838	1270	1760	2340	2980	3690	4500	5410
2.6	201	388	650	1000	1420	1930	2490	3130	3870	4700
2.8	157	308	524	817	1170	1620	2100	2660	3310	4060
3.0	127	251	433	681	982	1370	1800	2290	2860	3530
3.2	105	209	363	576	835	1180	1550	1980	2490	3090
3.4	88	175	307	490	714	1010	1340	1720	2170	2700
3.6	73	147	259	416	610	865	1150	1480	1880	2350
3.8	61	122	215	348	512	730	970	1260	1600	2010
4.0	42	86	154	250	371	533	711	926	1190	1500

Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.

R = radius of curve Vd = design speed e = rate of superelevation

Note: Use of emax = 4 percent should be limited to urban conditions.

Source: A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission.

TABLE 2.8 Minimum Radii for Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 6 Percent

e (%)	Vd = 15 mi/h R (ft)	Vd = 20 mi/h R (ft)	Vd = 25 mi/h R (ft)	Vd = 30 mi/h R (ft)	Vd = 35 mi/h R (ft)	Vd = 40 mi/h R (ft)	Vd = 45 mi/h R (ft)
1.5	868	1580	2290	3130	4100	5230	6480
2.0	614	1120	1630	2240	2950	3770	4680
2.2	543	991	1450	2000	2630	3370	4190
2.4	482	884	1300	1790	2360	3030	3770
2.6	430	791	1170	1610	2130	2740	3420
2.8	384	709	1050	1460	1930	2490	3110
3.0	341	635	944	1320	1760	2270	2840
3.2	300	566	850	1200	1600	2080	2600
3.4	256	498	761	1080	1460	1900	2390
3.6	209	422	673	972	1320	1740	2190
3.8	176	358	583	864	1190	1590	2010
4.0	151	309	511	766	1070	1440	1840
4.2	131	270	452	684	960	1310	1680
4.4	116	238	402	615	868	1190	1540
4.6	102	212	360	555	788	1090	1410
4.8	91	189	324	502	718	995	1300
5.0	82	169	292	456	654	911	1190
5.2	73	152	264	413	595	833	1090
5.4	65	136	237	373	540	759	995
5.6	58	121	212	335	487	687	903
5.8	51	106	186	296	431	611	806
6.0	39	81	144	231	340	485	643

(Continued)

e	Vd = 50 mi/h	Vd = 55 mi/h	II o о 3 &	Vd = 65 mi/h	Vd = 70 mi/h	Vd = 75 mi/h	Vd = 80 mi/h
(%)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)
1.5	7870	9410	11100	12600	14100	15700	17400
2.0	5700	6820	8060	9130	10300	11500	12900
2.2	5100	6110	7230	8200	9240	10400	11600
2.4	4600	5520	6540	7430	8380	9420	10600
2.6	4170	5020	5950	6770	7660	8620	9670
2.8	3800	4580	5440	6200	7030	7930	8910
3.0	3480	4200	4990	5710	6490	7330	8260
3.2	3200	3860	4600	5280	6010	6810	7680
3.4	2940	3560	4250	4890	5580	6340	7180
3.6	2710	3290	3940	4540	5210	5930	6720
3.8	2490	3040	3650	4230	4860	5560	6320
4.0	2300	2810	3390	3950	4550	5220	5950
4.2	2110	2590	3140	3680	4270	4910	5620
4.4	1940	2400	2920	3440	4010	4630	5320
4.6	1780	2210	2710	3220	3770	4380	5040
4.8	1640	2050	2510	3000	3550	4140	4790
5.0	1510	1890	2330	2800	3330	3910	4550
5.2	1390	1750	2160	2610	3120	3690	4320
5.4	1280	1610	1990	2420	2910	3460	4090
5.6	1160	1470	1830	2230	2700	3230	3840
5.8	1040	1320	1650	2020	2460	2970	3560
6.0	833	1060	1330	1660	2040	2500	3050

Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.

R = radius of curve Vd = design speed e = rate of superelevation

Source: A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission.

TABLE 2.9 Minimum Radii for Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 8 Percent

e	Vd = 15 mi/h Vd	= 20 mi/h	Vd = 25 mi/h Vd	= 30 mi/h	Vd = 35 mi/h	II 4^ О 3 &	Vd = 45 mi/h
(%)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)
1.5	932	1640	2370	3240	4260	5410	6710
2.0	676	1190	1720	2370	3120	3970	4930
2.2	605	1070	1550	2130	2800	3570	4440
2.4	546	959	1400	1930	2540	3240	4030
2.6	496	872	1280	1760	2320	2960	3690
2.8	453	796	1170	1610	2130	2720	3390
3.0	415	730	1070	1480	1960	2510	3130
3.2	382	672	985	1370	1820	2330	2900
3.4	352	620	911	1270	1690	2170	2700
3.6	324	572	845	1180	1570	2020	2520
3.8	300	530	784	1100	1470	1890	2360
4.0	277	490	729	1030	1370	1770	2220
4.2	255	453	678	955	1280	1660	2080
4.4	235	418	630	893	1200	1560	1960
4.6	215	384	585	834	1130	1470	1850
4.8	193	349	542	779	1060	1390	1750
5.0	172	314	499	727	991	1310	1650
5.2	154	284	457	676	929	1230	1560
5.4	139	258	420	627	870	1160	1480
5.6	126	236	387	582	813	1090	1390
5.8	115	216	358	542	761	1030	1320
6.0	105	199	332	506	713	965	1250
6.2	97	184	308	472	669	909	1180
6.4	89	170	287	442	628	857	1110
6.6	82	157	267	413	590	808	1050
6.8	76	146	248	386	553	761	990
7.0	70	135	231	360	518	716	933
7.2	64	125	214	336	485	672	878
7.4	59	115	198	312	451	628	822
7.6	54	105	182	287	417	583	765
7.8	48	94	164	261	380	533	701
8.0	38	76	134	214	314	444	587

e	Vd = 50 mi/h	Vd = 55 mi/h	II C О 3 &	Vd = 65 mi/h	Vd = 70 mi/h	Vd = 75 mi/h	Vd = 80 mi/h
(%)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)
1.5	8150	9720	11500	12900	14500	16100	17800
2.0	5990	7150	8440	9510	10700	12000	13300
2.2	5400	6450	7620	8600	9660	10800	12000
2.4	4910	5870	6930	7830	8810	9850	11000
2.6	4490	5370	6350	7180	8090	9050	10100
2.8	4130	4950	5850	6630	7470	8370	9340
3.0	3820	4580	5420	6140	6930	7780	8700
3.2	3550	4250	5040	5720	6460	7260	8130
3.4	3300	3970	4700	5350	6050	6800	7620
3.6	3090	3710	4400	5010	5680	6400	7180
3.8	2890	3480	4140	4710	5350	6030	6780
4.0	2720	3270	3890	4450	5050	5710	6420
4.2	2560	3080	3670	4200	4780	5410	6090
4.4	2410	2910	3470	3980	4540	5140	5800
4.6	2280	2750	3290	3770	4310	4890	5530
4.8	2160	2610	3120	3590	4100	4670	5280
5.0	2040	2470	2960	3410	3910	4460	5050
5.2	1930	2350	2820	3250	3740	4260	4840
5.4	1830	2230	2680	3110	3570	4090	4640
5.6	1740	2120	2550	2970	3420	3920	4460
5.8	1650	2010	2430	2840	3280	3760	4290
6.0	1560	1920	2320	2710	3150	3620	4140
6.2	1480	1820	2210	2600	3020	3480	3990
6.4	1400	1730	2110	2490	2910	3360	3850
6.6	1330	1650	2010	2380	2790	3240	3720
6.8	1260	1560	1910	2280	2690	3120	3600
7.0	1190	1480	1820	2180	2580	3010	3480
7.2	1120	1400	1720	2070	2470	2900	3370
7.4	1060	1320	1630	1970	2350	2780	3250
7.6	980	1230	1530	1850	2230	2650	3120
7.8	901	1140	1410	1720	2090	2500	2970
8.0	758	960	1200	1480	1810	2210	2670

Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.

R = radius of curve Vd = design speed e = rate of superelevation

Source: A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission.

TABLE 2.10 Minimum Radii for Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 10 Percent

e Vd	= 15 mi/h Vd	= 20 mi/h	Vd = 25 mi/h Vd	= 30 mi/h	Vd = 35 mi/h	II 4^ О 3 &	Vd = 45 mi/h
(%)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)
1.5	947	1680	2420	3320	4350	5520	6830
2.0	694	1230	1780	2440	3210	4080	5050
2.2	625	1110	1600	2200	2900	3680	4570
2.4	567	1010	1460	2000	2640	3350	4160
2.6	517	916	1330	1840	2420	3080	3820
2.8	475	841	1230	1690	2230	2840	3520
3.0	438	777	1140	1570	2060	2630	3270
3.2	406	720	1050	1450	1920	2450	3040
3.4	377	670	978	1360	1790	2290	2850
3.6	352	625	913	1270	1680	2150	2670
3.8	329	584	856	1190	1580	2020	2510
4.0	308	547	804	1120	1490	1900	2370
4.2	289	514	756	1060	1400	1800	2240
4.4	271	483	713	994	1330	1700	2120
4.6	255	455	673	940	1260	1610	2020
4.8	240	429	636	890	1190	1530	1920
5.0	226	404	601	844	1130	1460	1830
5.2	213	381	569	802	1080	1390	1740
5.4	200	359	539	762	1030	1330	1660
5.6	188	339	511	724	974	1270	1590
5.8	176	319	484	689	929	1210	1520
6.0	164	299	458	656	886	1160	1460
6.2	152	280	433	624	846	1110	1400
6.4	140	260	409	594	808	1060	1340
6.6	130	242	386	564	772	1020	1290
6.8	120	226	363	536	737	971	1230
7.0	112	212	343	509	704	931	1190
7.2	105	199	324	483	671	892	1140
7.4	98	187	306	460	641	855	1100
7.6	92	176	290	437	612	820	1050
7.8	86	165	274	416	585	786	1010
8.0	81	156	260	396	558	754	968
8.2	76	147	246	377	533	722	930
8.4	72	139	234	359	509	692	893
8.6	68	131	221	341	486	662	856
8.8	64	124	209	324	463	633	820
9.0	60	116	198	307	440	604	784
9.2	56	109	186	291	418	574	748
9.4	52	102	175	274	395	545	710
9.6	48	95	163	256	370	513	671
9.8	44	87	150	236	343	477	625
10.0	36	72	126	200	292	410	540

(Continued)

e Vd	= 50 mi/h	Vd = 55 mi/h	II o О 3 &	Vd = 65 mi/h	Vd = 70 mi/h	Vd = 75 mi/h	Vd = 80 mi/h
(%)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)
1.5	8280	9890	11700	13100	14700	16300	18000
2.0	6130	7330	8630	9720	10900	12200	13500
2.2	5540	6630	7810	8800	9860	11000	12200
2.4	5050	6050	7130	8040	9010	10100	11200
2.6	4640	5550	6550	7390	8290	9260	10300
2.8	4280	5130	6050	6840	7680	8580	9550
3.0	3970	4760	5620	6360	7140	7990	8900
3.2	3700	4440	5250	5930	6680	7480	8330
3.4	3470	4160	4910	5560	6260	7020	7830
3.6	3250	3900	4620	5230	5900	6620	7390
3.8	3060	3680	4350	4940	5570	6260	6990
4.0	2890	3470	4110	4670	5270	5930	6630
4.2	2740	3290	3900	4430	5010	5630	6300
4.4	2590	3120	3700	4210	4760	5370	6010
4.6	2460	2970	3520	4010	4540	5120	5740
4.8	2340	2830	3360	3830	4340	4900	5490
5.0	2240	2700	3200	3660	4150	4690	5270
5.2	2130	2580	3060	3500	3980	4500	5060
5.4	2040	2460	2930	3360	3820	4320	4860
5.6	1950	2360	2810	3220	3670	4160	4680
5.8	1870	2260	2700	3090	3530	4000	4510
6.0	1790	2170	2590	2980	3400	3860	4360
6.2	1720	2090	2490	2870	3280	3730	4210
6.4	1650	2010	2400	2760	3160	3600	4070
6.6	1590	1930	2310	2670	3060	3480	3940
6.8	1530	1860	2230	2570	2960	3370	3820
7.0	1470	1790	2150	2490	2860	3270	3710
7.2	1410	1730	2070	2410	2770	3170	3600
7.4	1360	1670	2000	2330	2680	3070	3500
7.6	1310	1610	1940	2250	2600	2990	3400
7.8	1260	1550	1870	2180	2530	2900	3310
8.0	1220	1500	1810	2120	2450	2820	3220
8.2	1170	1440	1750	2050	2380	2750	3140
8.4	1130	1390	1690	1990	2320	2670	3060
8.6	1080	1340	1630	1930	2250	2600	2980
8.8	1040	1290	1570	1870	2190	2540	2910
9.0	992	1240	1520	1810	2130	2470	2840
9.2	948	1190	1460	1740	2060	2410	2770
9.4	903	1130	1390	1670	1990	2340	2710
9.6	854	1080	1320	1600	1910	2260	2640
9.8	798	1010	1250	1510	1820	2160	2550
10.0	694	877	1090	1340	1630	1970	2370

Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.

R = radius of curve Vd = design speed e = rate of Superelevation

Source: A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission.

TABLE 2.11 Minimum Radii for Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 12 Percent

e	Vd = 15 mi/h Vd	= 20 mi/h	Vd = 25 mi/h Vd	= 30 mi/h	Vd = 35 mi/h	II О 3	Vd = 45 mi/h
(%)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)
1.5	950	1690	2460	3370	4390	5580	6910
2.0	700	1250	1820	2490	3260	4140	5130
2.2	631	1130	1640	2250	2950	3750	4640
2.4	574	1030	1500	2060	2690	3420	4240
2.6	526	936	1370	1890	2470	3140	3900
2.8	484	863	1270	1740	2280	2910	3600
3.0	448	799	1170	1620	2120	2700	3350
3.2	417	743	1090	1510	1970	2520	3130
3.4	389	693	1020	1410	1850	2360	2930
3.6	364	649	953	1320	1730	2220	2750
3.8	341	610	896	1250	1630	2090	2600
4.0	321	574	845	1180	1540	1980	2460
4.2	303	542	798	1110	1460	1870	2330
4.4	286	512	756	1050	1390	1780	2210
4.6	271	485	717	997	1320	1690	2110
4.8	257	460	681	948	1260	1610	2010
5.0	243	437	648	904	1200	1540	1920
5.2	231	415	618	862	1140	1470	1840
5.4	220	395	589	824	1090	1410	1760
5.6	209	377	563	788	1050	1350	1690
5.8	199	359	538	754	1000	1300	1620
6.0	190	343	514	723	960	1250	1560
6.2	181	327	492	694	922	1200	1500
6.4	172	312	471	666	886	1150	1440
6.6	164	298	452	639	852	1110	1390
6.8	156	284	433	615	820	1070	1340
7.0	148	271	415	591	790	1030	1300
7.2	140	258	398	568	762	994	1250
7.4	133	246	382	547	734	960	1210
7.6	125	234	366	527	708	928	1170
7.8	118	222	351	507	684	897	1130
8.0	111	210	336	488	660	868	1100

e Vd	= 15 mi/h	Vd = 20 mi/h	Vd = 25 mi/h	Vd = 30 mi/h	Vd = 35 mi/h	II 4^ О 3 &	Vd = 45 mi/h
(%)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)
8.2	105	199	321	470	637	840	1070
8.4	100	190	307	452	615	813	1030
8.6	95	180	294	435	594	787	997
8.8	90	172	281	418	574	762	967
9.0	85	164	270	403	554	738	938
9.2	81	156	259	388	535	715	910
9.4	77	149	248	373	516	693	883
9.6	74	142	238	359	499	671	857
9.8	70	136	228	346	481	650	832
10.0	67	130	219	333	465	629	806
10.2	64	124	210	320	448	608	781
10.4	61	118	201	308	432	588	757
10.6	58	113	192	296	416	568	732
10.8	55	108	184	284	400	548	707
11.0	52	102	175	272	384	527	682
11.2	49	97	167	259	368	506	656
11.4	47	92	158	247	351	485	629
11.6	44	86	149	233	333	461	600
11.8	40	80	139	218	312	434	566
12.0	34	68	119	188	272	381	500

(Continued)

TABLE 2.11 Minimum Radii for Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 12 Percent (Continued)

e	Vd = 50 mi/h Vd	= 55 mi/h	Vd = 60 mi/h	Vd = 65 mi/h	Vd = 70 mi/h	Vd = 75 mi/h	Vd = 80 mi/h
(%)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)
1.5	8370	9990	11800	13200	14800	16400	18100
2.0	6220	7430	8740	9840	11000	12300	13600
2.2	5640	6730	7930	8920	9980	11200	12400
2.4	5150	6150	7240	8160	9130	10200	11300
2.6	4730	5660	6670	7510	8420	9380	10500
2.8	4380	5240	6170	6960	7800	8700	9660
3.0	4070	4870	5740	6480	7270	8110	9010
3.2	3800	4550	5370	6060	6800	7600	8440
3.4	3560	4270	5030	5690	6390	7140	7940
3.6	3350	4020	4740	5360	6020	6740	7500
3.8	3160	3790	4470	5060	5700	6380	7100
4.0	2990	3590	4240	4800	5400	6050	6740
4.2	2840	3400	4020	4560	5130	5750	6420
4.4	2700	3240	3830	4340	4890	5490	6120
4.6	2570	3080	3650	4140	4670	5240	5850
4.8	2450	2940	3480	3960	4470	5020	5610
5.0	2340	2810	3330	3790	4280	4810	5380
5.2	2240	2700	3190	3630	4110	4620	5170
5.4	2150	2590	3060	3490	3950	4440	4980
5.6	2060	2480	2940	3360	3800	4280	4800
5.8	1980	2390	2830	3230	3660	4130	4630
6.0	1910	2300	2730	3110	3530	3990	4470
6.2	1840	2210	2630	3010	3410	3850	4330
6.4	1770	2140	2540	2900	3300	3730	4190
6.6	1710	2060	2450	2810	3190	3610	4060
6.8	1650	1990	2370	2720	3090	3500	3940
7.0	1590	1930	2290	2630	3000	3400	3820
7.2	1540	1860	2220	2550	2910	3300	3720
7.4	1490	1810	2150	2470	2820	3200	3610
7.6	1440	1750	2090	2400	2740	3120	3520
7.8	1400	1700	2020	2330	2670	3030	3430
8.0	1360	1650	1970	2270	2600	2950	3340

e Vd	= 50 mi/h	Vd = 55 mi/h	Vd = 60 mi/h	Vd = 65 mi/h	Vd = 70 mi/h	Vd = 75 mi/h	Vd = 80 mi/h
(%)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)	R (ft)
8.2	1320	1600	1910	2210	2530	2880	3260
8.4	1280	1550	1860	2150	2460	2800	3180
8.6	1240	1510	1810	2090	2400	2740	3100
8.8	1200	1470	1760	2040	2340	2670	3030
9.0	1170	1430	1710	1980	2280	2610	2960
9.2	1140	1390	1660	1940	2230	2550	2890
9.4	1100	1350	1620	1890	2180	2490	2830
9.6	1070	1310	1580	1840	2130	2440	2770
9.8	1040	1280	1540	1800	2080	2380	2710
10.0	1010	1250	1500	1760	2030	2330	2660
10.2	980	1210	1460	1720	1990	2280	2600
10.4	951	1180	1430	1680	1940	2240	2550
10.6	922	1140	1390	1640	1900	2190	2500
10.8	892	1110	1350	1600	1860	2150	2460
11.0	862	1070	1310	1560	1820	2110	2410
11.2	831	1040	1270	1510	1780	2070	2370
11.4	799	995	1220	1470	1730	2020	2320
11.6	763	953	1170	1410	1680	1970	2280
11.8	722	904	1120	1350	1620	1910	2230
12.0	641	807	1000	1220	1480	1790	2130

Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.

R = radius of curve Vd = design speed e = rate of superelevation

Source: A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission.

a different maximum superelevation rate. Table 2.7 shows values for a maximum rate of 0.04; Table 2.8, for 0.06; Table 2.9, for 0.08; Table 2.10, for 0.10; and Table 2.11, for 0.12. Method 5 was used to calculate the minimum radius for each superelevation rate less than the maximum rate in each design speed column in the tables.

The superelevation rates on low-speed urban streets are set using method 2 described above, in which side friction is used to offset the effect of centrifugal force up to the maximum friction value allowed for the design speed. Superelevation is then introduced for sharper curves. The design data in Table 2.12, based on method 2 and a maximum superelevation rate of 0.04, can be used for low-speed urban streets and temporary roads. The design data in Table 2.13 can be used for a wider range of design speeds and superelevation rates.

In attempting to apply the recommended superelevation rates for low-speed urban roadways, various factors may combine to make these rates impractical to obtain. These factors include wide pavements, adjacent development, drainage conditions, and frequent access points. In such cases, curves may be designed with reduced or no superelevation, although crown removal is the recommended minimum.

Effect of Grades on Superelevation. On long and fairly steep grades, drivers tend to travel somewhat slower in the upgrade direction and somewhat faster in the downgrade direction than on level roadways. In the case of divided highways, where each pavement can be superelevated independently, or on one-way roadways such as ramps, this tendency should be recognized to see whether some adjustment in the superelevation rate would be desirable and/or feasible. On grades of 4 percent or greater with a length of 1000 ft (305 m) or more and a superelevation rate of 0.06 or more, the designer may adjust the superelevation rate by assuming a design speed 5 mi/h (8 km/h) less in the upgrade direction and 5 mi/h (8 km/h) greater in the downgrade direction, provided that the assumed design speed is not less than the legal speed. On two-lane, two-way roadways and on other multilane undivided highways, such adjustments are less feasible, and should be disregarded.

Superelevation Methods. There are three basic methods for developing superelevation on a crowned pavement leading into and coming out of a horizontal curve. Figure 2.9 shows each method. In the most commonly used method, case I, the pavement edges are revolved about the centerline. Thus, the inner edge of the pavement is depressed by half of the superelevation and the outer edge raised by the same amount. Case II shows the pavement revolved about the inner or lower edge of pavement, and case III shows the pavement revolved about the outer or higher edge of pavement. Case II can be used where off-road drainage is a problem and lowering the inner pavement edge cannot be accommodated. The superelevation on divided roadways is achieved by revolving the pavements about the median pavement edge. In this way, the outside (high side) roadway uses case II, while the inside (low side) roadway uses case III. This helps control the amount of “distortion” in grading the median area.

Superelevation Transition. The length of highway needed to change from a normal crowned section to a fully superelevated section is referred to as the superelevation transition. This length is shown as X in Fig. 2.9, which also shows the various other elements described below. The superelevation transition is divided into two parts: the tangent runout, and the superelevation runoff.

The tangent runout (T in Fig. 2.9) is the length required to remove the adverse pavement cross slope. As is shown for case I of Fig. 2.9, this is the length required to raise the outside edge of pavement from a normal cross slope to a half-flat section. The superelevation runoff (L in Fig. 2.9) is the length required to raise the outside

TABLE 2.12 Superelevation Rates and Runoff Lengths (ft) for Horizontal Curves on Low-Speed Urban Streets Based on a Maximum Superelevation Rate of 4 Percent

Design speed, mi/h

20 25 30 35 40 45

Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.

Source: Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with

permission.

TABLE 2.13 Runoff Lengths (ft) for Horizontal Curves with Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 12 Percent Based on One Lane Rotated about the Centerline

e Vd	= 15 mi/h	Vd = 20 mi/h	Vd = 25 mi/h	Vd = 30 mi/h	Vd = 35 mi/h	II О 3	Vd = 45 mi/h
(%)	L (ft)	L (ft)	L (ft)	Lr (ft)	L (ft)	Lr (ft)	L (ft)
1.5	0	0	0	0	0	0	0
2.0	31	32	34	36	39	41	44
2.2	34	36	38	40	43	46	49
2.4	37	39	41	44	46	50	53
2.6	40	42	45	47	50	54	58
2.8	43	45	48	51	54	58	62
3.0	46	49	51	55	58	62	67
3.2	49	52	55	58	62	66	71
3.4	52	55	58	62	66	70	76
3.6	55	58	62	65	70	74	80
3.8	58	62	65	69	74	79	84
4.0	62	65	69	73	77	83	89
4.2	65	68	72	76	81	87	93
4.4	68	71	75	80	85	91	98
4.6	71	75	79	84	89	95	102
4.8	74	78	82	87	93	99	107
5.0	77	81	86	91	97	103	111
5.2	80	84	89	95	101	108	116
5.4	83	88	93	98	105	112	120
5.6	86	91	96	102	108	116	124
5.8	89	94	99	105	112	120	129
6.0	92	97	103	109	116	124	133
6.2	95	101	106	113	120	128	138
6.4	98	104	110	116	124	132	142
6.6	102	107	113	120	128	137	147
6.8	105	110	117	124	132	141	151
7.0	108	114	120	127	135	145	156
7.2	111	117	123	131	139	149	160
7.4	114	120	127	135	143	153	164
7.6	117	123	130	138	147	157	169
7.8	120	126	134	142	151	161	173
8.0	123	130	137	145	155	166	178
8.2	126	133	141	149	159	170	182
8.4	129	136	144	153	163	174	187
8.6	132	139	147	156	166	178	191
8.8	135	143	151	160	170	182	196
9.0	138	146	154	164	174	186	200
9.2	142	149	158	167	178	190	204
9.4	145	152	161	171	182	194	209
9.6	148	156	165	175	186	199	213
9.8	151	159	168	178	190	203	218
10.0	154	162	171	182	194	207	222
10.2	157	165	175	185	197	211	227
10.4	160	169	178	189	201	215	231
10.6	163	172	182	193	205	219	236
10.8	166	175	185	196	209	223	240
11.0	169	178	189	200	213	228	244
11.2	172	182	192	204	217	232	249
11.4	175	185	195	207	221	236	253
11.6	178	188	199	211	225	240	258
11.8	182	191	202	215	228	244	262
12.0	185	195	206	218	232	248	267

(Continued)

TABLE 2.13 Runoff Lengths (ft) for Horizontal Curves with Design Speeds from 15 to 80 mi/h (24 to 129 km/h) and Superelevation Rates to 12 Percent Based on One Lane Rotated about the Centerline (Continued)

e V	= 50 mi/h	Vd = 55 mi/h	Vd = 60 mi/h	Vd = 65 mi/h	Vd = 70 mi/h	Vd = 75 mi/h	Vd = 80 mi/h
(%)	Lr (ft)	Lr (ft)	Lr (ft)	Lr (ft)	Lr (ft)	Lr (ft)	Lr (ft)
1.5	0	0	0	0	0	0	0
2.0	48	51	53	56	60	63	69
2.2	53	56	59	61	66	69	75
2.4	58	61	64	67	72	76	82
2.6	62	66	69	73	78	82	89
2.8	67	71	75	78	84	88	96
3.0	72	77	80	84	90	95	103
3.2	77	82	85	89	96	101	110
3.4	82	87	91	95	102	107	117
3.6	86	92	96	100	108	114	123
3.8	91	97	101	106	114	120	130
4.0	96	102	107	112	120	126	137
4.2	101	107	112	117	126	133	144
4.4	106	112	117	123	132	139	151
4.6	110	117	123	128	138	145	158
4.8	115	123	128	134	144	152	165
5.0	120	128	133	140	150	158	171
5.2	125	133	139	145	156	164	178
5.4	130	138	144	151	162	171	185
5.6	134	143	149	156	168	177	192
5.8	139	148	155	162	174	183	199
6.0	144	153	160	167	180	189	206
6.2	149	158	165	173	186	196	213
6.4	154	163	171	179	192	202	219
6.6	158	169	176	184	198	208	226
6.8	163	174	181	190	204	215	233
7.0	168	179	187	195	210	221	240
7.2	173	184	192	201	216	227	247
7.4	178	189	197	207	222	234	254
7.6	182	194	203	212	228	240	261
7.8	187	199	208	218	234	246	267
8.0	192	204	213	223	240	253	274
8.2	197	209	219	229	246	259	281
8.4	202	214	224	234	252	265	288
8.6	206	220	229	240	258	272	295
8.8	211	225	235	246	264	278	302
9.0	216	230	240	251	270	284	309
9.2	221	235	245	257	276	291	315
9.4	226	240	251	262	282	297	322
9.6	230	245	256	268	288	303	329
9.8	235	250	261	273	294	309	336
10.0	240	255	267	279	300	316	343
10.2	245	260	272	285	306	322	350
10.4	250	266	277	290	312	328	357
10.6	254	271	283	296	318	335	363
10.8	259	276	288	301	324	341	370
11.0	264	281	293	307	330	347	377
11.2	269	286	299	313	336	354	384
11.4	274	291	304	318	342	360	391
11.6	278	296	309	324	348	366	398
11.8	283	301	315	329	354	373	405
12.07	288	306	320	335	360	379	411

Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.

Source: A Policy on Geometric Design of Highways and Streets, American Association of State Highway and Transportation Officials, Washington, D. C., 2004, with permission.

NOTE: The diagrams below show positioning of the superelevation transition for both simple curves and spiral curves. Only one of these conditions would exist for a given transition.

LEGEND: X = Length of superelevation transition.

L = Length of superelevation runoff.

T = Tangent runout R = Crown removal

G = Equivalent slope rate of Change of outside pavement edge compared to the control line In each case. (See Table 2.13 for values.)

N = Normal cross slope S = Full superelevation rate

FIGURE 2.9 Superelevation transition between tangent and simple or spiral curves for three cases. (From Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with permission) edge of pavement from a half-flat section to a fully superelevated section. The length of transition required to remove the pavement crown (R in Fig. 2.9) is generally equal to twice the T distance.

The minimum superelevation transition length X should be equal in feet to 3 times the design speed in miles per hour. This includes the tangent runout (T) as previously described. The reason to specify this minimum is to avoid the appearance of a “kink” in
the roadway that a shorter transition would provide. The distance is approximately equal to that traveled by a vehicle in 2 s at design speed. This requirement does not apply to low-speed roadways, temporary roads, superelevation transitions near intersections, or transitions between adjacent horizontal curves (reverse or same direction) where normal transitions would overlap each other. In these cases, the minimum transition length is determined by multiplying the edge of pavement correction by the equivalent slope rate (G) shown in Table 2.14. The rate of change of superelevation should be constant throughout the transition X. Some agencies use a flatter rate of transition through the T or R sections than that recommended in Table 2.14, an acceptable but unnecessary practice.

The values given for Lr in Tables 2.12 and 2.13 are based on one 12-ft (3.66-m) lane revolved about the centerline. Table 2.14 shows methods of calculating L when more lanes are revolved about the centerline. In the equations in Table 2.14, L is substituted for Lr. In addition to the terms described in Fig. 2.9, two additional ones are used. W is the width from the point of revolution to the outside edge of pavement. For example, if three 12-ft (3.66-m) lanes are revolved about the lane edge between lanes 2 and 3, then W = 3 X 12 = 36 ft (11 m); the wider section of pavement is used for the width. B is an adjustment factor for multilane pavements to allow for some reduction in the superelevation transition for roads other than interstates, freeways, expressways, and ramps. Section (a) in Table 2.14 lists the equivalent slope rate values G for the various design speeds. Section (b) provides the multilane adjustments factors B for the speeds. Section (c) calculates the value of the overall transition length X based on the values given in (a) and (b) along with a given W and S for each case in Fig. 2.9. Finally, section (d) tests the values calculated to ensure that the minimum transition length discussed in this section is provided. Values for X, L, and T can be lengthened if necessary to achieve a 2-s transition time.

Superelevation Position. Figure 2.9 shows the recommended positioning of the proposed superelevation transition in relationship to the horizontal curve. For those curves with spirals, the transition from adverse crown removal to full superelevation should occur within the limits of the spiral. In other words, the spiral length should equal the L value, usually rounded to the nearest 25 ft (7.6 m).

For simple curves without spirals, the L transition should be placed so that 50 to 70 percent of the maximum superelevation rate is outside the curve limits (point of curvature PC to point of tangency PT). It is recommended that whenever possible, two-thirds of the full superelevation rate be present at the PC and PT. See the case diagrams in Fig. 2.9 for a graphic presentation of the recommended positioning.

Profiles and Elevations. Breakpoints at the beginning and end of the superelevation transition should be rounded to obtain a smooth profile. One suggestion is to use a “vertical curve” on the edge of the pavement profile with a length in feet equal to the design speed in mi/h (i. e., 45 ft for 45 mi/h). The final construction plans should have the superelevation tables or pavement details showing the proposed elevations at the centerline, pavement edges, and, if applicable, lane lines or other breaks in the cross slopes. Pavement or lane widths should be included where these widths are in transition. Pavement edge profiles should be plotted to an exaggerated vertical profile within the limits of the superelevation transitions to check calculations and to determine the location of drainage basins. Adjustments should be made to obtain smooth profiles. Special care should be taken in determining edge elevations in a transition area when the profile grade is on a vertical curve.

Superelevation between Reverse Horizontal Curves. When two horizontal curves are in close proximity to each other, the superelevation transitions calculated independently

TABLE 2.14 Superelevation Notes for Adjusting Runoff Lengths in Tables 2.12 and 2.13

(a) Maximum relative gradients for profiles between the edge of pavement and the centerline or reference line

Design speed, mi/h	Relative gradient	Equivalent slope rate, G
20	0.74	135:1
25	0.70	143:1
30	0.66	152:1
35	0.62	161:1
40	0.58	172:1
45	0.54	185:1
50	0.50	200:1
55	0.47	213:1
60	0.45	222:1
65	0.43	233:1
70	0.40	250:1

(b) Transition length adjustment factors for wide pavements

Number of lanes	B for interstates, freeways,	B for
from point of rotation	expressways, and ramps	other roadways
1.0	1.00	1.00
1.5	1.00	0.83
2.0	1.00	0.75
2.5	1.00	0.70
3.0	1.00	0.67
3.5	1.00	0.64
(c) Calculate X, L, T
Case I	Cases II and III
X = BW(S + N)G	X = BWSG
L = BWSG	L = BW(S – N/2)G
T = BWNG	T = BW(N/2)G

(d) Check for 2-second minimum transition

(Note: D is the linear ft equivalent of the design speed in mi/h. For example, D = 60 ft for 60 mi/h)

If X > 3D, then the values for X, L, and T from section (c) are valid.

If X < 3D, then recalculate X, L, and T as follows:

Case I	Cases II and III
X = 3D	X = 3D
L = 3D[S/(N + S)]	L = 3D[(2S – N)/2S]
T = 3D[N/(N + S)]	T = 3D(N/2S)

Conversion: 1 mi/h = 1.609 km/h.

General notes:

1. The Lr in Tables 2.12 and 2.13 is the same as L in Table 2.14 and is based on a two-lane 24-ft pavement revolved about the centerline.

2. Adjustments to L for varying two-lane pavement widths can be made by direct proportion. For a 20-ft pavement revolved about the centerline, L’ = L(20/24).

3. Determination of X, L, and T when more than one lane is revolved about the centerline (or other reference line, such as a baseline or edge of pavement) is shown in part (c). Values for G and B in the formulas are given in parts (a) and (b), respectively. The value for W is the pavement width from the point of rotation to the farthest edge.

4. The minimum length of superelevation transition (X) as discussed in the text is the distance traveled in 2 s. This number can be rounded off to a figure in feet equal to 3 times the design speed. In part (d) the calculated X value is compared to the value of 3D, where D is the linear feet equivalent of the design speed in miles per hour. If the value of 3D is larger, X is set equal to this value and L and T are adjusted accordingly.

5. The L value is also the recommended spiral length where spirals are used.

Source: Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with

permission.

may overlap each other. In these cases, the designer should coordinate the transitions to provide a smooth and uniform change from the full superelevation of the first curve to the full superelevation of the second curve. Figure 2.10 shows two diagrams suggesting ways in which this may be accomplished. In both diagrams each curve has its own L value (L1, L2) depending on the degree of curvature, and the superelevation is revolved about the centerline.

PAV	‘EMENT REVOLVED ABC LI	3UT THE CENTERLINE L2	—
JL.	-50Lito. TOLi,	.50L2to. T0L2	—– .—————– —–
	D.

—	PT«		® PCI	—_______ d) 2 ———————-
S.-5 Ut SIMPLE CURVES

PA	VEMENT REVOLVED ABOUT THE CENTERLINE . L3	—
LI		L2
	D


CS«I	ST[1]I		TS	SC*2
SPIRAL CURVES

LEGEND:

(A) – Centerline Pavement (D – Outside EP. Curve I,

Inside EP. Curve 2 E. P.=Edge of Pavement

L3 = Total Superelevation Transition between Spiral Curves

FIGURE 2.10 Superelevation transition between reverse horizontal curves, simple or spiral. (From Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with permission)

The top diagram involves two simple curves. In the case of new or relocated alignment, the PT of the first curve and the PC of the second curve should be separated by enough distance to allow a smooth, continuous transition between the curves at a rate not exceeding the G value for the design speed (Table 2.14). This requires that the distance be not less than 50 percent nor greater than 70 percent of L1 + L2. Two-thirds is the recommended portion. When adapting this procedure to existing curves where no alignment revision is proposed, the transition should conform as closely as possible to the above criteria. When the available distance between the curves is less than 50 percent of L1 + L2, the transition rate may be increased and/or the superelevation rate at the PT or PC may be set to less than 50 percent of the full superelevation rate.

The lower diagram involves two spiral curves. Where spiral transitions are used, the spiral-to-tangent (ST) point of the first curve and the tangent-to-spiral (TS) transition of the second curve may be at, or nearly at, the same location, without causing superelevation problems. In these cases, the crown should not be reestablished as shown in Fig. 2.9, but instead, both pavement edges should be in continual transition between the curves, as shown in the lower diagram of Fig. 2.10. The total superelevation transition length is the distance between the curve-to-spiral (CS) point of the first curve and spiral-to-curve (SC) point of the second curve.

Spiral Transitions. When a motor vehicle enters or leaves a circular horizontal curve, it follows a transition path during which the driver makes adjustments in steering to account for the gain or loss in centrifugal force. For most curves, the average driver can negotiate this change in steering within the normal width of the travel lane. However, combinations of higher speeds and sharper curvature may cause the driver to move into an adjacent travel lane while accomplishing the change. To prevent this occurrence, the designer should use spirals to smooth out transitions.

There are several advantages to using spiral transitions for horizontal curves:

• They provide an easy-to-follow path for the driver to negotiate.

• They provide a convenient area in which to place the superelevation transition.

• They provide an area where the pavement width can be transitioned when required for curve widening.

• They provide a smoother appearance to the driver.

The Euler spiral is the one most commonly used in highway design. The degree of curve varies gradually from zero at the tangent end to the degree of the circular arc at the curve end. By definition, the degree of curve at any point along the spiral varies directly with the length measured along the spiral. In the case where a spiral transition connects two simple curves, the degree of curve varies directly from that of the first circular arc to that of the second circular arc. As a general guideline, spirals should be used on roadways where the design speed is 50 mi/h (80 km/h) or greater and the degree of curvature exceeds the values given in Table 2.15 for various design speeds listed.

Horizontal Alignment Considerations. The following items should be considered when establishing new horizontal alignment: •

TABLE 2.15 Maximum Curve without a Spiral

Design speed, mi/h	Design speed, km/h	Max. degree of curve	Min. radius, ft	Min. radius, m
50	80	4°30′	1273	388
55	88	3°45′	1528	466
60	96	3°00′	1910	582
65	105	2°30′	2292	699
70	113	2°15′	2546	776

Source: Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with permission.

• Tangents and/or flat curves should be provided on high, long fills.

• Compound curves should be used only with caution.

• Abrupt alignment reversals should be avoided.

• Two curves in the same direction separated by a short tangent (broken-back or flat – back curves) should be avoided.

Sight Distance

Posted by admin on 12/ 11/ 15

A primary feature in the design of any roadway is the availability of adequate sight distance for the driver to make decisions while driving. In the articles that follow, the text contains conclusions based on information contained in Ref. 1. Derivation of formulas and references to supporting research are contained in that document and will not be repeated here. The reader is encouraged to consult that document for more detailed background information. The following paragraphs discuss various sight distances and the role they play in the design of highways.

Stopping Sight Distance. Stopping sight distance is the distance ahead that a motorist should be able to see so that the vehicle can be brought safely to a stop short of an obstruction or foreign object on the road. This distance will include the driver’s reaction or perception distance and the distance traveled while the brakes are being applied. The total distance traveled varies with the initial speed, the brake reaction time, and the coefficient of friction for wet pavements and average tires. The values in Table 2.2 were developed using a reaction time of 2.5 s and a braking deceleration rate of 11.2 ft/s2 (3.4 m/s2). The height of eye was taken as 3.50 ft (1.07 m) and the height of the object as 2.00 ft (0.61 m).

When considering the effect of stopping sight distance, it is necessary to check both the horizontal and the vertical stopping sight distance. Horizontal sight distance may be restricted on the inside of horizontal curves by objects such as bridge piers, buildings, concrete barriers, guiderail, cut slopes, etc. Figure 2.6 shows a diagram describing how horizontal sight distance is checked along an extended curve. Both formulas and a nomograph are provided to enable a solution. Many times, where the curve is not long enough or there are a series of roadway horizontal curves, a plotted-out “graphic” solution will be required to determine the available horizontal sight distance.

TABLE 2.2 Stopping Sight Distance (SSD) for Design Speeds from 20 to 70 mi/h (32 to 113 km/h)

Design speed, mi/h	Design SSD, ft	Design speed, mi/h	Design SSD, ft
20	115	46	375
21	120	47	385
22	130	48	400
23	140	49	415
24	145	50	425
25	155	51	440
26	165	52	455
27	170	53	465
28	180	54	480
29	190	55	495
30	200	56	510
31	210	57	525
32	220	58	540
33	230	59	555
34	240	60	570
35	250	61	585
36	260	62	600
37	270	63	615
38	280	64	630
39	290	65	645
40	305	66	665
41	315	67	680
42	325	68	695
43	340	69	715
44	350	70	730
45	360

Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.

Source: Location and Design Manual, Vol. 1, Roadway Design,

Ohio Department of Transportation, with permission.

SIGHT DISTANCE

FIGURE 2.6 Horizontal sight distance along curve. Conversion: 1 ft = 0.305 m. (From Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with permission)

When a cut slope is the potential restriction, the offset should be measured to a point on the backslope having the same elevation as the average of the roadway where the driver is, and the location of the lane downstream where a potential hazardous object lies. In this way, an allowance of 2.75 ft (0.84 m) of vegetative growth on the backslope can be made, since the driver’s eye is assumed to be 3.5 ft (1.07 m) above the pavement and the top of a 2.0-ft (0.61-m) hazardous object downstream may still be seen.

Vertical sight distance may be restricted by the presence of vertical curves in the roadway profile. The sight distance on a crest vertical curve is based on a driver’s
ability to see a 2.0-ft-high (0.61-m) object in the roadway without being blocked by the pavement surface. The height of eye for the driver used in the calculations is 3.5 ft (1.07 m).

The sight distance on a sag vertical curve is dependent on the driver’s being able to see the pavement surface as illuminated by headlights at night. The height of the headlight is assumed to be 2.0 ft (0.61 m), and the height of the object is 0.0. The upward divergence angle of the headlight beam is assumed to be 1°.

Intersection Sight Distance. A motorist attempting to enter or cross a highway from a stopped condition should be able to observe traffic at a distance that will allow safe movement. In cases where traffic is intermittent or moderate in flow, the motorist will wait to find an acceptable “gap.” The driver approaching the intersection on the through road should have a clear view of the intersection including any vehicles stopped, waiting to cross, or turning. The methods described in the following paragraphs produce distances that provide sufficient sight distance for the stopped driver to make a safe crossing or turning maneuver. If these distances cannot be obtained, the minimum sight distance provided should not be less than the stopping sight distance for the through roadway. This would allow a driver on the through roadway adequate time to bring the vehicle to a stop if the waiting vehicle started to cross the intersection and suddenly stopped or stalled. If this distance cannot be provided, additional safety measures must be provided. These could include, but are not limited to, advance warning signals and flashers and/or reduced speed limit zones in the vicinity of the intersection.

There are three possible maneuvers for a motorist stopped at an intersection to make. The motorist can (1) cross the intersection by clearing oncoming traffic on both the left and right of the crossing vehicle, (2) turn left into the crossing roadway after first clearing the traffic on the left and then making a safe entry into the traffic stream from the right, or (3) turn right into the crossing roadway by making a safe entry into the traffic stream from the left.

In order to evaluate the amount of sight distance available to a stopped vehicle waiting to make a crossing or turning maneuver, the American Association of State Highway and Transportation Officials (AASHTO) adopted the concept of using “sight triangles” (Ref. 1). The vertices of the triangles are (a) the waiting driver’s position, (b) the approaching driver’s position, and (c) the intersection of the paths of the two vehicles, assuming a straight-ahead path for the waiting vehicles. Figure 2.7 shows the concept of sight triangles, emphasizing both the horizontal and vertical elements to be considered. The shaded area in the triangles is to be free of objects that would obstruct the field of vision for either driver. The profile view shows the limiting effect of vertical curvature of the through roadway. Notice that the height of eye of the drivers (3.50 ft or 1.07 m) is used for both the waiting and approaching vehicles. This stresses the importance of both drivers being able to see each other.

Table 2.3A provides intersection sight distance values for through vehicle speeds from 15 to 70 mi/h (24 to 113 km/h). The distances are based on a time gap of 7.5 s for a passenger vehicle turning left and a gap of 6.5 s for a crossing or right-turning vehicle. The height of eye and object were taken as 3.50 ft (1.07 m). The table also provides K values for crest vertical curves that would provide the required sight distance. (See Art. 2.2.4 for a discussion of vertical curvature.) Formulas are provided so that distances can be calculated for trucks requiring a longer time gap and for time adjustments due to upgrades or multiple lane crossings. See the notes in Table 2.3A, which explain how to adjust the timings.

Passing Sight Distance. In Table 2.3B, the “PSD” column lists the distances required for passing an overtaken vehicle at various design speeds. These distances are applicable

Подпись: WITH PAVEMENT AS OBSTRUCTION

Sight Distance PORTION OF ABUTMENT
AS OBSTRUCTION

FIGURE 2.7 Intersection sight triangles. (a) Sight triangles. (b) Vertical components. a1 = the distance, along the minor road, from the decision point to 12 the lane width of the approaching vehicle on the major road. a2 = the distance, along the minor road, from the decision point to 112 the lane width of the approaching vehicle on the major road. b = intersection sight distance (ISD). d = the distance from the edge of the traveled way of the major road to the decision point; the distance should be a minimum of 14.4 ft (4.39 m) and 17.8 ft (5.43 m) preferred. (From Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with permission) to two-lane roadways only. Among the assumptions that affect the required distance calculations are (1) the passing vehicle averages 10 mi/h (1.61 km/h) faster than the vehicle being passed, (2) the vehicle being passed travels at a constant speed and this speed is the average running speed (which is less than the design speed), and (3) the oncoming vehicle is traveling at the same speed as the passing vehicle. Table 2.3B contains K values for designing crest vertical curves to provide passing sight distance. These values assume that the height of the driver’s eye is 3.5 ft (1.07 m) for both the passing and the oncoming vehicle. The equations at the bottom of the table provide mathematical solutions for sight distance on the crest curves.

On two-lane roadways, it is important to provide adequate passing sight distance for as much of the project length as possible to compensate for missed opportunities due to oncoming traffic in the passing zone. On roadways where the design hourly traffic volume exceeds 400, the designer should investigate the effect of available passing sight distance on highway capacity using procedures outlined in the latest Transportation Research Board “Highway Capacity Manual” (Ref. 10). If the available passing sight distance restricts the capacity from meeting the design level of service requirement, then adjustments should be made to the profile to increase the distance.

Подпись: TABLE 2.3A Intersection Sight Distance (ISD) for Design Speeds from 15 to 70 mi/h (24 to 113 km/h) Design speed, mi/h Passenger cars completing a left turn from a stop (assuming a tg of 7.5 s) Passenger cars completing a right turn from a stop or crossing maneuver (assuming a tg of 6.5 s) ISD, ft K-crest vertical curve ISD, ft K-crest vertical curve 15 170 10 145 8 20 225 18 195 14 25 280 28 240 21 30 335 40 290 30 35 390 54 335 40 40 445 71 385 53 45 500 89 430 66 50 555 110 480 82 55 610 133 530 100 60 665 158 575 118 65 720 185 625 140 70 775 214 670 160

If ISD cannot be provided due to environmental or R/W constraints, then as a minimum, the SSD for vehicles on the major road should be provided.

Подпись: ISD = 1.47 X V. Xt major g Using S = intersection sight distance L = length of crest vertical curve A = algebraic difference in grades (%), absolute value K = rate of vertical curvature

• For a given design speed and an A value, the calculated length L = K X A.

• To determine S with a given L and A, use the following:

For S < L: S = 52.92 VK, where K = L/A For S > L: S = 1400/A + L/2

Note: For design criteria pertaining to collectors and local roads with ADT less than 400, please refer to Ref. 15, Guidelines for Geometric Design of Very Low-Volume Local Roads (ADT < 400).

Time gaps

Time gap(s) at design

Design vehicle speed of major road (tg), s

A. Left turn from a stop	Passenger car	7.5
	Single-unit truck	9.5
	Combination truck	11.5
B. Right turn from a	Passenger car	6.5
stop or crossing	Single-unit truck	8.5
maneuver	Combination truck	10.5

(Continued)

TABLE 2.3A Intersection Sight Distance (ISD) for Design Speeds from 15 to 70 mi/h (24 to 113 km/h) (Continued)

A. Note: The ISD and time gaps shown in the above tables are for a stopped vehicle to turn left onto a two-lane highway with no median and grades of 3 percent or less. For other conditions, the time gap must be adjusted as follows:

• For multilane highways: For left turns onto two-way highways with more than two lanes, add 0.5 s for passenger cars or 0.7 s for trucks for each additional lane, from the left, in excess of one, to be crossed by the turning vehicle.

• For minor road approach grades: If the approach grade is an upgrade that exceeds 3 percent, add 0.2 s for each percent grade for left turns.

B. Note: The ISD and time gaps shown in the above tables are for a stopped vehicle to turn right onto a two-lane highway with no median and grades of 3 percent or less. For other conditions, the time gap must be adjusted as follows:

• For multilane highways: For crossing a major road with more than two lanes, add 0.5 s for passenger cars or 0.7 s for trucks for each additional lane to be crossed and for narrow medians that cannot store the design vehicle.

• For minor road approach grades: If the approach grade is an upgrade that exceeds 3 percent, add 0.1 s for each percent grade.

Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.

Source: Location and Design Manual, Vol. 1, Roadway Design, Ohio

Department of Transportation, with permission.

If the problem cannot be resolved in this manner, then consideration should be given to providing passing lane sections or constructing a multilane facility.

Decision Sight Distance. Stopping sight distances are usually sufficient to allow reasonably competent drivers to come to a hurried stop under ordinary circumstances. However, these distances may not be sufficient for drivers when information is difficult to perceive, or when unexpected maneuvers are required. In these circumstances, the decision sight distance provides a greater length for drivers to reduce the likelihood of error in receiving information, making decisions, or controlling the vehicle.

The following are examples of locations where it is desirable to provide decision sight distance: (1) exit ramps, (2) diverging roadway terminals, (3) intersection stop bars, (4) changes in cross section, such as toll plazas and lane drops, and (5) areas of concentrated demand where there is apt to be “visual noise” (i. e., where sources of information compete, such as roadway elements, traffic, traffic control devices, and advertising signs).

Table 2.4 shows decision sight distances based on design speed and avoidance maneuvers. The table lists values for five different avoidance maneuvers. Maneuvers A (rural stop) and B (urban stop) are calculated similar to the standard stopping sight distance values, except that perception times are increased to 3.0 s for rural environment and 9.1 s for urban. For maneuvers C (rural area), D (suburban area), and E (urban area), the braking component is replaced by an avoidance maneuver. This can be a change in speed, path, or direction. Values shown are calculated based on distance traveled during the perception-maneuver time. This time varies with speed and ranges from 10.2 to 10.7 s for rural areas, 12.1 to 12.4 s for suburban areas, and 14.0 to 14.1 s for

TABLE 2.3B Minimum Passing Sight Distance (PSD) for Design Speeds from 20 to 70 mi/h (32 to 113 km/h)

PSD

Design speed, mi/h	Minimum PSD, ft	K-crest vertical curve
20	710	180
25	900	289
30	1090	424
35	1280	585
40	1470	772
45	1625	943
50	1835	1203
55	1985	1407
60	2135	1628
65	2285	1865
70	2480	2197

Using S = minimum passing sight distance L = length of crest vertical curve A = algebraic difference in grades (%), absolute value K = rate of vertical curvature

• For a given design speed and an A value, the calculated length L = K X A.

• To determine S with a given L and A, use the following:

For S < L: S = 52.92 VK, where K = L/A. For S > L: S = 1400/A + L/2.

Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.

Source: Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with permission.

urban areas. To calculate available distance on a crest vertical curve, the driver’s eye height is 3.5 ft (1.07 m) and the height of the object to be avoided is 2.0 ft (0.61 m).

Where conditions call for the use of a decision sight distance in design that cannot be achieved, every effort should be made to provide the stopping sight distance values from Table 2.2. Consideration should also be given to using suitable traffic control devices to provide advance warning of the unexpected conditions that may be encountered.

GEOMETRIC DESIGN

Posted by admin on 12/ 11/ 15

2.2.1 Design Controls

Once a route has been selected for a new highway, or a decision has been made to perform major work on an existing facility, the next step is to establish the design controls. The various factors considered for design controls may be generally grouped into five categories: functional classification, traffic data, terrain, locale, and design speed.

Functional classification is a way of grouping roadways together by the character of service they provide. The initial division is between urban and rural roadways. The urban classification may be defined differently in various parts of the country, but one definition is incorporated areas having a population of 5000 or more (Ref. 1). Rural areas are those areas outside of urban areas.

Each of these may be further subdivided into other classifications defined as follows:

Interstate. Roadways on the federal system with the highest design speeds and the highest design standards.

Freeway. An expressway with full access control and no at-grade intersections. Expressway. A divided arterial highway with full or partial control of access and generally having grade separations at major intersections.

Arterial. A facility primarily used for through traffic, usually on a continuous route.

Collector. An intermediate roadway system which connects arterials with the local road or street systems.

Local road or street. A road whose primary function is to provide access to residences, businesses, or other abutting properties.

Traffic data are an important foundation in highway design. The information used in design is usually a future forecast on the basis of existing traffic counts and expanded on the basis of normal expected growth in the area or enhanced by estimates of future business, commercial, or residential development. Most highway designs are based on what traffic demands will be 20 years from the current year. Shorter time periods, such as 10 years, may apply to resurfacing projects or other minor repair projects. It is important that within the same jurisdiction traffic data be forecast using the same methods and techniques, in order to ensure similar designs for similar type roadways. This is especially true for roadways in a given state jurisdiction.

The following types of traffic numbers are used most frequently in design:

Average daily traffic (ADT). The average number of vehicles using a roadway in a 24-hour period.

Design hourly volume (DHV). The estimated number of vehicles using the roadway in the 30th highest hour of the year. This number is generally 8 to 12 percent of the ADT and is used extensively in determining lane widths and shoulder characteristics of the roadway cross section.

Directional design hourly volume (DDHV). The estimated number of vehicles traveling in one direction of a two-way roadway in the 30th highest hour of the year. This number must be at least 50 percent of the DHV and is usually in the range of 50 to 60 percent. A higher value would indicate that the roadway is a major link in the commuter network, carrying a heavy inbound load in the morning and reversing that flow in the evening.

Truck percentage (T). The portion of the ADT which consists of B and C trucks. Traffic counts are usually separated according to vehicle type:

P = passenger cars (%)

A = commercial (%), consisting of light delivery trucks, panel trucks, and pickup trucks

B = commercial (%), consisting of semitrailer and truck-trailer combinations

C = commercial (%), consisting of buses or dual-tired trucks having single or tandem rear axles

Traffic counts sometimes group the P and A vehicles together and the B and C together.

Terrain is a factor that can significantly influence design features, especially in rural areas. Various categories of terrain are level, rolling, and hilly. They are further described as follows:

Level terrain. Any combination of grades and horizontal and vertical alignment permitting heavy vehicles to maintain approximately the same speed as passenger cars. Grades are generally limited to 1 or 2 percent.

Rolling terrain. Any combination of grades and horizontal and vertical alignment causing heavy vehicles to reduce their speeds substantially below those of passenger cars, but not to operate at crawl speeds.

Hilly terrain. Any combination of grades and horizontal and vertical alignment causing heavy vehicles to operate at crawl speed.

Heavy vehicles are defined as any vehicle having a weight (pounds) to horsepower ratio of 200 or greater (Ref. 1). Crawl speed is defined as the maximum sustained speed heavy vehicles can maintain on an extended upgrade. See Ref. 1 for graphs showing the effect of grades on acceleration and deceleration of heavy vehicles.

Locale describes the character and extent of development in the vicinity. It can be considered commercial, industrial, or residential, as well as rural or urban.

Design speed is defined as “a selected speed used to determine the various geometric design features of the roadway” (Ref. 1). When designing new or reconstructed roadways, the design speed should always equal or exceed the proposed legal speed of the roadway.

Table 2.1 (Ref. 7) shows the relationship of the functional classification, traffic data, terrain, locale, and design speed to the various geometric design features listed on the chart.

It should be noted that there are situations when it will not be possible or reasonable to meet the design standard for a particular feature in a given project. When this occurs, the designer must bring this to the attention of the reviewing authority for approval of what is being proposed, or suggestions on what other course of action to take. A design exception must be approved by the reviewing authority when a substandard feature is allowed to remain as part of the design. In this way, it can be documented that this was not an error or oversight on the part of the designer and that every effort has been made to provide the best design possible in the given situation.

Detail Design Phase

Posted by admin on 12/ 11/ 15

During the detail design phase, various design elements are finalized and construction plans are developed. Project development in this phase can include many intermediate reviews prior to final plan submission. These may include some or all of the following, depending on the complexity of the plan:

Traffic request/validation Traffic signal warrant analysis Airway-highway clearance study Alignment, grade, and typical section review Conceptual maintenance of traffic review Structure type study Retaining wall justification Service road justification Preliminary drainage review Preliminary right-of-way review Bridge type, size, and location study Drive review

Detail Design Phase

FIGURE 2.1 Example of map used in study of alternate routes showing four possible corridors. Conversions: 5 mi = 8 km, 2000 ft = 610 m. (From Justification Study for Crossroad Grade Separations, US 30, by Balke Engineers for Ohio Department of Transportation, with permission)

ALIGNMENT

Ml RELOCATION

_C0NRAIL

|E<fenvi]|»"

-J

го

<-C~

ALIGNMENT C

£crWj.’ J

LEGEND

Residence With Farm Buildings

Residence Only

Commercial Facility

Residence With Potential Historic Significance

Overpass

Road Closure tcul-de-sac)

Unr^n.

Detail Design Phase

.I»,SHAFER ROAD

©	LEGEND Residence Wilh Farm Buildings
	Residence Only
©	Commercial Facility
©	Residence With Potential Historic Significance
an	Overpass
•	Road Closure (cul-de-sac)

BARTHOLD ROAD –y

jOUAKER ROAD

ВUCYRUS BYPASS;

RIWEHARTROAD-

jSHROLLROAD

L – Jtr nil

I US 30

CR S5

NEVADA-WYNFORD ROAD

со

_CONRA|L

CR 2

ВЦCYRUS-NEVAPA ROADI

Detail Design Phase

6610

.1GNMENT D

:|SR 182f:

Lsx-

CONftAH

iZfpP

>Ь : ЕЗєпуіііє"" O’

■рь

<1 TR 55 |

ALIGNMENT C

180 = Estimated 2000 ADT 270 = Estimated 2020 APT

Detail Design Phase

;Гц

2840

4250

6700

10500

US 30

BARTHOLD ROAD^

BUCYRUS BYPASS’

RINEHART ROAD

,SHRQLL ROAD

I US 30

NEVADA-WYMFQRD ROAD J–‘

J CR 18 Г

-J

сл

_CONRAIL

BUCYRUS-NEVADA HO АРІ

Detail Design Phase

Slope review Traffic control Lighting Waterline Sanitary sewer

Final roadway, field and office check

This is not intended to be an all-inclusive list. The designer should contact the government agency having review and final acceptance authority to see what reviews are required during this phase of plan development.

Following acceptance of the final plans, specifications, and estimates, the project is processed for letting. Any necessary consent legislation is obtained. The project is then advertised, bids are taken, and the construction contract is awarded.

Preliminary Development Phase

Posted by admin on 12/ 11/ 15

Two types of projects are considered here: (1) projects that involve studies outside the existing corridor or where a facility for more than one alternative mode of transportation may be involved, and (2) projects where feasible alternatives are limited to the existing corridor but did not qualify to pass directly to the design phase. The main difference between the two as far as processing is concerned is that the first group has not yet narrowed its alternatives down to feasible alternatives.

In each case, a project inventory is developed. This information includes historical sites; public recreational facilities; school, church, fire, and police districts; proposed development; land use; existing and other proposed transportation facilities; preliminary traffic assignments; and other similar social, economic, and environmental features, which are pertinent to the area under study. Using this information as a guide, all preliminary alternatives are developed together with documentation of the anticipated effects on community, preliminary cost estimates, and other technical considerations. Advantages and disadvantages of each alternative are studied. Where appropriate, coordination with other modes is considered. The “no-build” alternative is also considered and provides a reference point for defining potential beneficial and adverse impacts. Public hearings are held to gain input from the local public in the affected areas. Following an evaluation of all input received, alternatives are weighed and only those considered to be feasible are forwarded to the next step. From this point on, all projects in the preliminary development phase are on the same path.

Among the environmental concerns which must be considered for each alternative are the following (see also Chap. 1):

Air quality. A study of the effect of a proposed transportation improvement on the quality of the air

Historic or prehistoric. A study of the effect of the proposed transportation improvement on historic or prehistoric objects or on lands or structures currently entered into the National Register or which may be eligible for addition to the National Register

Endangered species. A study of the effect of the proposed transportation improvement on rare or endangered plants or animals having national or state recognition Natural areas. A study of the effect of the proposed transportation improvement on natural areas designated as having regional, state, or national significance Parks and recreation. A study of the effect of the proposed transportation improvement on publicly owned parks, recreation areas, or wildlife and waterfowl refuges designated as having national, state, or local significance

Prime farmlands. A study of the effect of the proposed transportation improvement on farmlands with high productivity due to soil and water conditions or having other unique advantages for growing specialty crops

Scenic rivers. A study of the effect of the proposed transportation improvement on any scenic rivers of state or national significance

Streams and wetlands. A study of the effect of the proposed transportation improvement on streams and wetlands on project and abutting land areas

Water quality. A study of the effect of the proposed transportation improvement on the quality of live streams or bodies of water

The next step is a refinement of feasible alternatives. This requires additional work sufficient to prepare an environment document. This could include such items as approximate construction costs; alignment and profile studies; typical section development; preliminary designs for geometric layout, drainage, right-of-way, and utilities; location of interchanges, grade separations, and at-grade intersections; preliminary bridge designs at critical locations; channel work; air, noise, and water studies; flood hazard evaluations; and other supplemental studies and right-of-way information. Once again, input is sought from the public sector through advertisement and public hearings.

Figure 2.1 shows the corridors for the feasible alternatives for an 11-mi relocation of U. S. 30 in Ohio (Ref. 13). The map is part of a study evaluating crossroad treatment for each alternative. Figures 2.2 and 2.3 show the projected crossroad treatments for the various alternatives. The options are (1) interchange, (2) grade separation, or (3) closing roads with cul-de-sacs. Since the proposed segment will be a limited-access highway, the option of at-grade intersection was not considered. Figures 2.4 and 2.5 show current and 20-year projected traffic volumes for all roadways. These are examples of maps used in the study of feasible alternatives.

After consideration of all the input and comparing the benefits and disadvantages of each alternative, the next step is to make a selection of the recommended alternative. This selection is certified by the state’s transportation director. Following approval of the environmental document, the project may proceed to the design phase.

Project Evaluation

Posted by admin on 12/ 11/ 15

Once projects reach the selected lists, the next phase is project evaluation. This phase

will determine which projects can advance to detail design and which will require a

more detailed evaluation in preliminary development.

Projects that can advance directly to design phase meet the following criteria:

• No additional right-of-way (permanent or temporary) will be required to accomplish the work and there will be no adverse effect on abutting real properties.

• No major changes in the operation of access points, traffic volumes, traffic flows, vehicle mix, or traffic patterns.

• No involvement with a live stream or an intermittent stream having significant year – round pools, upstream or downstream, in the immediate vicinity.

• No involvement with a historic site.

Examples of these types of improvement are:

• Restoration and/or reconstruction of existing pavement surfaces

• Modernization of an existing facility by adding or widening shoulders

• Modernization of existing facilities by adding auxiliary lanes or pavement widening to accomplish a localized purpose (weaving, climbing, speed change, protected turn, etc.)

• Intersection improvements

• Reconstruction or rehabilitation of existing grade separation structures

• Reconstruction or rehabilitation of existing stream crossings which do not involve any modification of a live stream or otherwise affect the water quality

• Landscaping or rest area upgrading projects

• Lighting, signing, pavement marking, signalization, freeway surveillance and control systems, railroad protective devices, etc.

• Minor safety-type improvements, such as guiderail replacement or installation of breakaway sign hardware

• Outdoor advertising control programs

• Bicycle or pedestrian facilities provided within existing right-of-way

All projects that do not fall into the above categories must undergo additional evaluation in a preliminary development phase.

TRANSPORTATION DEVELOPMENT PROCESS

Posted by admin on 12/ 11/ 15

2.1.1 Statewide Systems Planning

The beginnings of any roadway project involving government money are found in a statewide transportation planning program. The state transportation department develops a set of goals and objectives which take into account social, economic, environmental, and developmental goals of other state, federal, and local agencies. Based on these goals and objectives, the department identifies transportation improvement needs throughout the state. The approach is from a multimodal standpoint; that is, not just highways are considered, but all forms of transportation, including public transportation, railroads, water, aviation, bikeways, and pedestrian ways (Ref. 6).

2.1.2 Transportation Programming Phase

In order to evaluate various projects from various parts of the state, information is collected consisting of the following items: transportation inventories, traffic analyses, modal forecasts, future system requirements, levels of service, population data and forecasts, land use inventories, public facilities plans, and basic social, economic, and environmental data. This information comes from various sources, both public and private, is updated on a regular basis, and is used in developing the state’s transportation improvement program.

The statewide fiscal program is also considered in developing the plan. Transportation investment, fiscal forecasts, and consideration of expenditure tradeoffs between modes are some of the financial considerations affecting the project selection process.

Public input is sought from regional to local levels. Local and regional planning organizations, as well as private individuals, have a chance to express opinions and provide input to the project selection process. Once all factors have been evaluated, the state announces and publishes its recommended transportation improvement plan. This usually consists of a one-year plan and a five-year plan, with remaining projects grouped under long-range plans.

HIGHWAY LOCATION,. DESIGN, AND TRAFFIC

Posted by admin on 12/ 11/ 15

Larry J. Shannon, P. E.

Highway Technical Manager ms Consultants Columbus, Ohio

This chapter begins with a description of the overall transportation development process, and then presents comprehensive information on the various elements of highway location and design. Included is the determination of horizontal and vertical alignment, with attention to obtaining proper sight distance and superelevation. The design of roadway cross sections, intersections, ramps, and service roads is addressed. Traffic aspects include an introduction to intelligent vehicle highway systems and the use of high-occupancy vehicle lanes. A presentation on preparation of highway construction plans and organizing CADD drawings is also provided. A list of references, which are noted in the text, concludes the chapter. Some design issues related to roadside safety are also discussed in Chap. 6.

End Uses in Highways

Posted by admin on 12/ 11/ 15

It is apparent that there are many uses of recycled materials in highway construction and related applications. Table 1.19 provides a summary of these uses for reference.

1.6.1 Recycling Hazardous Wastes

Under Subtitle C of RCRA, EPA has the authority to regulate recyclable hazardous waste material. It is critical to determine the type of waste and the proposed method of recycling in determining whether it is regulated under Subtitle C. The definition of solid waste under Section 261.2 identifies four types of recycling activities for which recycled wastes may be subject to Subtitle C regulation: use constituting disposal, burning waste-derived fuels for energy recovery, reclamation, and speculative reclamation.

Use Constituting Disposal. Use constituting disposal is defined as placing or applying a solid waste or a material contained in a product that was a solid waste on the land in a manner constituting disposal. In this case, land disposal regulations under RCRA Parts 264 and 265 apply. Use constituting disposal may include the following uses involved in the construction of highways or maintenance of highway landscaping: fill material, cover material, fertilizer, soil conditioner, dust suppressor, asphalt additive, and foundation material.

Burning and Blending of Waste Fuels. Burning and blending would be the applicable method for recycling used oil for fuel in asphalt plants. Used oil is not currently considered a hazardous waste unless it has a characteristic of ignitability, corrosivity, reactivity, or extraction procedure toxicity (ICRE characteristic). If the used oil is mixed with a hazardous waste, it is regulated as a hazardous waste fuel under RCRA, Part 266, Subpart D. Specifications for nonhazardous used oil fuel are described in Table 1.20. Used oils that do

Asphalt: Crop waste and other cellulose material may be reduced to an oil suitable for asphalt extender. Asphalt paving aggregate: Incinerator ash.

Asphalt mineral filler: Sewage sludge ash, fly ash, baghouse fines, cement kiln dust, lime waste. Asphalt-rubber binder: Scrap tires.

Asphalt stress-absorbing membranes: Scrap tires.

Asphalt rubberized crack sealant: Scrap tires.

Asphalt aggregate: Mill tailings, phosphogypsum, slag.

Asphalt fine aggregate: Glass and ceramics.

Asphalt cement modifier: Plastic waste.

Asphalt plant fuel: Used motor oil.

Asphalt paving: Bottom ash, boiler slag, blast furnace slag, steelmaking slag, nonferrous slag, reclaimed asphalt pavement, foundry sand, roofing shingle waste, petroleum-contaminated soils (after thermal treatment).

Base course: Glass and ceramic waste, construction and demolition debris, nonferrous slags, reclaimed asphalt pavement, reclaimed concrete pavement, mill tailings.

Pipe bedding: Foundry sand, glass, and ceramic waste.

Borrow material: Quarry waste, construction and demolition material.

Slope stabilization and erosion control: Sawdust and wood waste.

Mulch: Wood waste, paper waste (especially slick, magazine-type paper), compost.

Fertilizer: Animal manure and farm waste.

Embankments: Lumber and wood waste, sawdust and wood chips, recycled sanitary landfill refuse, fly ash, bottom ash, construction and demolition waste, sulfate waste, waste rock, mill tailings, coal refuse.

Cement stabilized base: Incinerator ash, fly ash, bottom ash, advanced SO2 control by-products, cement kiln dust, reclaimed asphalt pavement, petroleum-contaminated waste (after thermal treatment), coal refuse, and rice husk ash may be used as supplementary cementing material. Concrete: Incinerator ash from sewage sludge cake as vitrified aggregate or palletized aggregate. Lightweight fill material: Wood waste, sawdust, chipped wood, scrap tires.

Geotextile: Plastic waste.

Sealant: Scrap tires.

Safety hardware, fencing, signposts: Plastic wastes.

Flowable fill and grout: Quarry waste, fly ash.

Soil stabilization: Fly ash, advanced SO2 control by-product, cement kiln dust, lime waste. Antiskid material: Bottom ash, steelmaking slag.

Blasting grit: Nonferrous slags.

TABLE 1.20 Specification Levels for Used Oil Fuels

Specification	Maximum allowable level
Arsenic concentration	5 ppm
Cadmium concentration	2 ppm
Chromium concentration	10 ppm
Lead concentration	100 ppm
Flash point	1000°F
Total halogen concentration (unmixed)	4000 ppm
Total halogen concentration (mixed)	1000 ppm

Source: Adapted from Travis Wagner, Complete Handbook of Hazardous

Waste Regulation, Perry-Wagner Publishing, Brunswick, Maine, 1988, p. 46.

not meet one or all of these specifications and are not mixed with hazardous waste may still be burned in industrial boilers, but they must have an EPA identification number for this activity and must meet a higher standard of reporting than used oil meeting the specifications. A burner of either specification or off-specification used oil fuel must notify EPA of its used-oil-fuel activities and state the location and a general description of the used-oil – management activities. Copies of invoices and waste analysis conducted on the used oil must be maintained for at least 3 years.

Reclamation. Reclamation is the recovery of materials with value from a waste material and involves regeneration of waste material from the reclamation activities. Recovering precious metals from a waste stream (such as silver from x-ray film) is an example of reclamation. When the lead plates from lead-acid batteries are recovered, the activity is regulated under RCRA as reclamation. Use of material as feed stocks or ingredients in the production of a new product is not considered reclamation.

Speculative Accumulation. Any hazardous secondary material is considered a solid waste if accumulated before recycling unless 75 percent of the stockpile is recycled during a calendar year.

Domestic Waste

Posted by admin on 12/ 11/ 15

It is estimated that approximately 4 lb of domestic refuse is generated every day for every person in the United States, of which about 3 lb (1.4 kg) per day goes to domestic land-fills and 11 percent is recycled. It is estimated that about 185 million tons (168 X 109 kg) of domestic waste is generated per year in the United States. Several of these wastes have a potential for reuse in highways.

Refuse. Landfill refuse is not sought for reuse in highway construction because there is little homogeneity among landfill refuse, and so a great deal of analysis and separation would be required at individual landfills to determine the potential for use. However, there have been occasions when a highway right-of-way traverses a landfill. In such cases, analysis to find appropriate on-site placement of the refuse instead of costly relocation and disposal has been found to be cost-effective. The refuse was spread in thin layers and compacted into embankment material or used for raised medians.

Paper and Paperboard. Approximately 40 percent of the domestic waste generated in the United States is paper or cardboard. Approximately 25 percent of the wastepaper products are recycled each year and used primarily in making more paper, cardboard, and related materials. A highway use of wastepaper, particularly slick paper such as magazine paper, is in the production of mulch material.

Yard Waste and Compost. There are over 1400 yard waste composting stations in the country. Yard waste is banned completely from landfills in many states. Compost material must meet pathogen control, pH, metal concentration, nitrogen ratio, water-bearing capacity, maturity, particle size, and nutrient content control standards set by the EPA. Compost materials are used for mulching, soil amendment, fertilizers, and erosion control. Concerns related to leaching potential, odors, worker health and safety, long-term exposure, and public acceptance have limited use in highways to the experimental stage, except in landscape use.

Plastics. The amount of plastic waste generated each year is growing. Recycling plastics is complicated in that plastics are developed from at least six different resin bases, which must be sorted for the most-effective recycling. About 30 percent of the plastics made from polyethylene terephthalate (PET), the resin base of soda bottles, is recycled. One use of PET is as a geotextile. Low-density polyethylene (LDPE) resin from film and trash bags can be recycled into pellets for use as an asphalt modifier in paving mixes. High-density polyethylene (HOPE) from milk jugs has been used in manufacturing plastic posts. Reuse of commingled plastics is more difficult but has been applied in fencing and posts. Such plastics have also been used as traffic delineators.

Glass. The amount of glass containers produced each year is declining, but about

12.5 million tons (11.3 X 109 kg) of glass is disposed of as domestic waste each year. To be reused in glass manufacturing, glass must be sorted according to color. Uses in highways include as fine aggregate in unbound base courses, as pipe bedding, as aggregate in asphalt mixes, and as glass beads in traffic paint.

Ceramics. Ceramic waste consists of factory rejects and discarded housewares and plumbing fixtures. Only in infrequent instances are large quantities of waste ceramics available for reuse in large applications, such as highway projects. In California, crushed porcelain has been used as an unbound base course aggregate. Crushed porcelain has been found to meet or exceed quality requirements for concrete aggregate.

Incinerator Ash. Incinerator ash results from the burning of municipal waste. About 26 million tons (24 X 109 kg) of incinerator ash is produced each year, of which 90 percent is bottom ash and the remainder is fly ash. Fly ash often exceeds regulatory limits for concentrations of lead and cadmium. Fly ash is most often mixed with bottom ash, and this mixture generally does not contain sufficient concentrations of metals to render it hazardous. Incinerator ash has been used successfully as a partial replacement of coarse aggregate in asphalt mixtures, as roadway fill, and in base course construction when stabilized with Portland cement. Concerns on the part of the EPA about the leaching of heavy metals have initiated several studies.

Sewer Sludge Ash. More than 15,000 municipal wastewater treatment plants in the country produce over 8 million tons (7 X 109 kg) of dry solids of sewage sludge. Following dewatering, sludge cake contains between 18 and 24 percent solids consisting mostly of nitrogen and phosphorus, but may be contaminated from various wastewater streams. Much of this sludge cake is incinerated, producing about 1 million tons (0.9 X 109 kg) of ash a year. Sludge ash has the potential for use as an asphalt filler and use in brick manufacturing. Studies indicate that with heat treatment, the ash can produce lightweight pellets that can increase concrete compressive strength by 15 percent when replacing aggregate. Sewage sludge ash has been used as a mineral filler in asphalt paving in Iowa, Minnesota, and other states. Sewage sludge can be composted for agricultural uses such as soil amendments, compost, or fertilizer. Recycled municipal sewage sludge can be a health and safety concern for highway workers using it in landscaping.

Scrap Tires. In 1994, NCHRP published findings of a 5-year review and synthesis of all of the states’ highway practices involving the use of waste tires. This document, entitled Uses of Recycled Rubber Tires in Highways, is the result of a compilation of over 500 sources of information on the topic. The discussion in this section is a synopsis of the information provided in that document. A copy of the document can be obtained through the Transportation Research Board of the National Research Council 2101 Constitution Avenue NW, Washington, DC 20418.

It is estimated that 2 to 3 billion waste tires have accumulated in the United States, about 70 percent of which are dumped illegally throughout the countryside or disposed of in unauthorized, uncontrolled stockpiles. Also, scrap fires account for about 2 percent of the solid waste that is disposed in regulated landfills. Each year an additional 242 million more scrap tires add to the nation’s solid waste dilemma. Scrap tires are regulated under RCRA Subtitle D as a nonhazardous waste. However, if they are burned, the resulting residue, which may consist of oils, carbon black, and metal-concentrated ash, may be hazardous. In addition, leachate from tire-based products may also be a hazardous or toxic concern. Potential uses of scrap tires in highways and related facilities are numerous.

Table 1.17 identifies the uses of tires in transportation facilities in several states. The environmental implications of the use of scrapped tires in pavement are issues of emissions from the manufacture and placement of rubber asphalt. Leachate is also a major concern, particularly of metals (arsenic, barium, cadmium, chromium, lead, selenium, and zinc) and PAHs (polyaromatic hydrocarbons). A Minnesota study conducted in wetland areas concluded that the use of waste tires in asphalt-rubber pavements may affect groundwater quality. The study’s results were comparable to two other studies with regard to metal leachates, but PAH leachate concentrations were not confirmed by the other studies. Mitigation measures suggested in the Minnesota study would be to place tire materials only in unsaturated zones of the subgrade or fill areas and not below the water table or within surface water boundaries. A Wisconsin study that scrap, shredded, and crumbed tires were not hazardous, nor did they release significant amounts of priority pollutants. Several studies have indicated that the emissions in asphalt-rubber operations are not significantly higher than with conventional asphalt concrete. The one exception to this may be the release of methyl isobutyl ketone, which appears to be consistently slightly higher than with the conventional mixture. The results of these studies should be used with caution, in that the tires from which asphalt rubber is made are not of the same chemical composition, and are continuing to change. The rubber-asphalt formulation process also varies significantly, changing the emissions and leachable properties of the asphalt rubber. Comparison difficulties are compounded in that the composition and

Type of use State Description of use

Erosion use California Shoulder reinforcement

Channel slope protection

Advantages

Disposal Low cost Erosion control

Availability of tires Disposal

Disposal

Flatten side slope

Concerns

Visual acceptance by public

Labor intensive Cost

Pull-out values

Unloading

Leachate

Cost

Windbreaks Slope reinforcement Pending project Side slope fill

Louisiana Pennsylvania V ermont

Wisconsin California North Carolina Rhode Island Arizona

Experimental project Anchored timber walls Experimental retaining wall Experimental retaining wall

Membrane to control expansive subgrade soils Shoulder membrane Ditch membrane

Retaining wall

Less moisture fluctuations Seal out moisture Prevent cracking Ride quality Lower maintenance cost

Membrane

California

Oregon

Washington

Wisconsin

Routine use Routine use

Routine use on bridge decks Experimental use

Safety hardware	Colorado	Experimental project		Tires become projectiles
	Connecticut	Tire-sand inertial barrier	Disposal Low cost	Debris
			Maintenance	Deceleration of vehicle
	Oregon	Bases for tubular markers
	Pennsylvania	Pending projects
	Texas	Bases for vertical panel supports
Railroad crossings	Oregon	Routine use	Ease of installation Smooth Reduced maintenance Potential reuse
	Pennsylvania	Experimental only
Valve box coverings	Oregon		Ease of installation Reduced maintenance Easy to adjust Durability
Planks and posts	California	Laminated tires for planks and posts	Strength
	Ontario	Sound barrier walls	Durability	Burning
			Lightweight Sound loss	Smoke
Drainage material	Pennsylvania	Aggregate drain rock replacement	Water-draining Stable roadway	Leachate
Culvert	Vermont	Whole tires bound together to form	Cost
		culvert
Interlocking block	Minnesota	Erosion control, safety barriers,	Ease of installation
		retaining walls, dikes, levees	Shock absorbing Resist chemical damage Durability

Source: Adapted from Uses of Recycled Rubber Tires in Highways, National Cooperative Highway Research Program (NCHRP), Transportation Research Board, Washington,

D. C., 1994.

Common uses	Innovative uses
Fills and embankments	Railroad grade crossing
Erosion control	Valve box coverings
Shoulder stabilization	Drainable materials
Channel slope protection	Planks and posts
Windbreak	Culverts
Side slope fill Slope reinforcement Retaining wall Membranes Safety hardware Tire-sand inertial barrier	Interlocking blocks

Source: Based on National Cooperative Highway Research

Program (NCHRP), Transportation Research Board, Uses of Recycled Rubber Tires in Highways, Washington, D. C., 1994.

formulation processes for the conventional concrete asphalt that is being used for a standard vary tremendously also. Common and innovative uses of scrap tires are summarized in Table 1.18.

« Previous 1 … 34 35 36 37 38 … 40 Next »

Library builder

Library builder

Library builder

Library builder

Categories

Distributing of pipes

Soldering of metalplastic pipes

Visually -

Miniatyurizm of a modern shower cabin: style and convenience

Shower, sauna, disco

Concrete baths and Dade Design company sinks.

With what to begin repair in a bathroom

How truly to choose a bath

Brand new bath: elegantly and especially

Bathe in a bath in pleasure!

Category HIGHWAY ENGINEERING HANDBOOK

Horizontal Alignment and Superelevation

Sight Distance

GEOMETRIC DESIGN

Detail Design Phase

Preliminary Development Phase

Project Evaluation

TRANSPORTATION DEVELOPMENT PROCESS

HIGHWAY LOCATION,. DESIGN, AND TRAFFIC

End Uses in Highways

Domestic Waste