In engineering design and analysis, loads usually arise from natural events, such as floods, storms, or earthquakes, that occur randomly in time and in space. The conventional practice for measuring the reliability of a hydrosystems engineering infrastructure is the return period or recurrence interval. The return period is defined as the long-term average (or expected) time between two successive failure-causing events. In time-to-failure analysis (Chap. 5), an equivalent term is the mean time to failure. Simplistically, the return period is equal to the reciprocal of the probability of the occurrence of the event in any one time interval. For many hydrosystems engineering applications, the time interval chosen is 1 year so that the probability associated with the return period is the average annual failure probability. Frequency analysis using the annual maximum flood or rainfall series is a typical example of this kind. Hence the determination of return period depends on the time period chosen (Borgman, 1963). The main theoretical disadvantage of using return period is that reliability is measured only in terms of expected time of occurrence of loads without considering their interactions with the resistance (Melchers, 1999).
In fact, the conventional interpretation of return period can be generalized as the average time period or mean time of the system failure when all uncertainties affecting load and resistance are considered. In other words, the return period can be calculated as the reciprocal of the failure probability computed by Eq. (1.2). Based on this generalized notion of return period, the equivalent return period corresponding to the conventional return period under different levels of resistance uncertainty is shown in Fig. 1.7. As can be seen, the equivalent return period becomes shorter than the conventional return period, as anticipated, when resistance uncertainty increases. For example, with COV(R) = 5 percent, a hydrosystem designed with a 100-year return
|
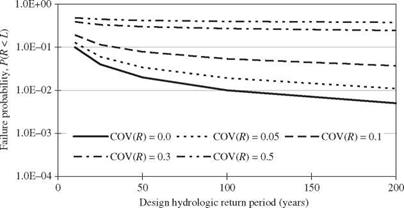
Figure 1.7 Equivalent return period versus design return period under COV(L) = 0.1.
|
TABLE 1.1 Different Types of Safety Factors
Type of safety
factor Definition
 Assigned number
Assigned number
rr /rl, where rr and rl are the true mean values of resistance and load R/L, where R and L are the mean values of resistance and load estimated from the available data
Ro/Lo, where Ro and Lo are the specified resistance and load 1/Y = Nl/Nr, where pf = P(L > yR) = P(NlL > NrR)
SOURCE: After Yen, 1979.
period under the conventional approach actually has about a 50-year return period.
Two other types of reliability measures that consider the relative magnitudes of resistance and anticipated load (called design load) are used frequently in engineering practice. One is the safety margin (SM), defined as the difference between the resistance and the anticipated load, that is,
SM = R – L (1.4)
The other is called the safety factor (SF), a ratio of resistance to load defined as
SF = R/L (1.5)
Several types of safety factors are summarized in Table 1.1, and their applications to engineering systems are discussed by Yen (1979).
Preassigned safety factor. This is an arbitrarily chosen safety factor that is used conventionally without probabilistic consideration. The value chosen largely depends on the designer’s subjective judgment with regard to the amount of uncertainty involved in his or her determination of design load and the level of safety desired.
Central safety factor. Owing to the fact that both resistance and load could be subject to uncertainty, the safety factor defined by Eq. (1.5), in fact, is a quantity subject to uncertainty as well. The central safety factor rsf is defined as
RSF = R R /RL (1.6)
in which rr and rl are the true mean values of resistance and load, respectively. In practice, values of rr and rl cannot be obtained precisely from the limited data. Therefore, rsf is only of theoretical interest.
Mean safety factor. If the estimated means of R and L on the basis of data are R and L, respectively, the mean safety factor (SF) is defined as
 SF = R/L
SF = R/L
Characteristic safety factor. Often in a project the significant design values of the parameters are not the mean values but specified values (or range of values). For example, the load used in a spillway design is not the mean value of all the floods nor the mean value of the selected floods of an annual maximum series. It may be simply a specified flood of a given magnitude (e. g., a flood with a 100-year return period). Therefore, the characteristic safety factor (SFc) can be defined as
SFc = Ro/Lo (1.8)
in which Ro and Lo are the specified resistance and load, respectively. If Ro and Lo both are assigned without a probabilistic analysis, Eq. (1.8) is identical to Eq. (1.5). If Ro and Lo are taken to be the mean values of resistance and load, Eq. (1.8) would become like Eq. (1.6) or Eq. (1.7). In general, Ro and Lo can be determined through a probabilistic analysis. For example, Tang and Yen (1972) use the estimated mean of resistance and the specified load, that is,
SFc = R/Lo (1.9)
to develop a risk-safety factor relationship in storm sewer design. Tung and Mays (1981) used the 100-year flood from the frequency analysis for Lo in developing risk-safety factor curves for a levee system.
Partial safety factor. The preceding safety factors apply to the total load and resistance of the system. It is possible, however, that different components in the system may be subject to different degrees of uncertainty. A smaller value of the safety factor can be assigned to those elements or components associated with less uncertainty than those with more uncertainty. In Table 1.1, NR and NL are the separate safety factors assigned to the resistance and load, respectively.
Theoretically, any one of the safety factors can be applied for its quantitative evaluation. However, the central safety factor is only of theoretical importance because in practice the exact distributions and values of the coefficient of variation are not known but estimated. Among the other four definitions, which one is preferred would depend on the nature of the problem. Clearly, these safety factors can be modified and refined. They are not mutually exclusive and can be made complementary. An in-depth comparative investigation of these factors in view of infrastructural system engineering applications would be desirable.














 Assigned number
Assigned number







