Yes, a good beam is a thing of beauty, but the main quality we are looking for in a beam is that it will not fail under the load we are asking it to carry. So we had better know a bit about the kinds of failures that can happen.
The failure in beams that people seem to grasp most easily is that of bending failure. If we keep loading a beam, particularly towards the middle of the span, we are placing ever greater bending stresses upon it. When we exceed the bending
strength of the beam, it will break, usually somewhere in the middle third of the span. This seems logical and natural, just as it seems natural that the two-by-eight plank described above is far more likely to break under a bending load if it is laid flat than if it is installed, properly, on edge. But common sense aside, it is useful to know why this is so from a structural or mathematical standpoint.
Because of a strength characteristic with the rather imposing name of section modulus, the depth (d) of the beam — the vertical dimension — has its value squared. But the breadth (b) of the beam carries only a regular linear value. For beams with rectilinear cross-sections, section modulus (S) is expressed: S = bd2/6. Interestingly, section modulus is solely a function of shape — geometry, if you like… and not a function of materials.
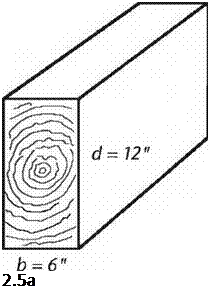
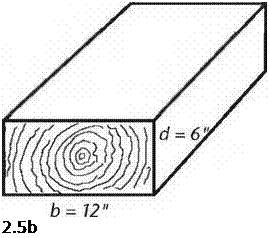
This strength relationship can be shown clearly if we look at the example of a timber with a 6-inch by 12-inch cross-section, because the constant — 6 — cancels out so conveniently. In Fig. 2.5a, we see a section of a six-by-twelve beam installed as it should be. The section modulus is the breadth (b, or 6") times the depth (d, or 12") squared, all divided by the constant 6. S = 6" X (12")2/6 = 144 inches cubed, the unit for section modulus (not to be confused with cubic inches.) On the bottom (Fig. 2.5b), the beam has been installed by a builder, who, to put it kindly, “is as thick as two short planks.” Now the breadth is 12 inches and the depth is 6 inches. So: S = 12" X (6")2/6 = 72 inches cubed. Now, mathematically, we can see that the beam is only half as strong in bending if we lay it down instead of standing it up correctly. I chose a six-by-twelve for easy math with whole numbers, but this relationship is true with any beam that is twice as deep as it is wide. With something like a two-by-ten joist, the difference is more extreme: the joist is five times stronger on bending installed “standing up” instead of “lying down.” The section modulus for a truly square beam or girder, like an eight-by-eight or ten-by-ten, can make use of the same formula, but as b and d are the same, it can be simplified to S = d5/6.
