BASIC OFFSETS

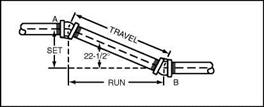
Basic offsets are all based on the use of right triangles. You now know about Set and Travel. It is time that you learned about a term known as Run. Travel, as I said earlier, is the distance between center of two offset fittings that cre­ates the length of a piece of pipe. This pipe’s length is determined as it devel­ops from fitting to fitting, traveling along the angle of the offset. When you want to know the Run, you are interested in the distance measured along a straight line from the bottom horizontal pipe. Refer to Fig. 2.4 for an example

FIGURE 2.3 ■ Decimal equivalents of fractions of an inch.

of what I’m talking about. Run is a term applied to the horizontal measurement from the center of one offset fitting to the center of the other offset fitting.

Most charts and tables assign letters to terms used in formulas. For our purposes, let’s establish our own symbols. We will call the letter S—Set, the letter R-Run, and the letter T—Travel. What are common offsets in the plumbing and pipe fitting trade? A 45° offset is the most common. Two other offsets sometimes use are 60° bends and 22V2° bends. These are the three most frequently used offsets and the ones that we will concentrate our efforts on.

The use of the right triangle is important when dealing with piping off­sets. The combination of Set, Travel, and Run form the triangle. I can provide you with a table that will make calculating offsets easier (Fig. 2.5), but you must still do some of the math yourself, or at least know some of the existing figures. This may seem a bit intimidating, but it is not as bad as you might think. Let me explain.

As a working plumber or pipe fitter, you know where your first pipe is. In our example earlier, where there was ductwork that needed to be cleared, you can easily determine what the measurement of the higher pipe must be. This might be determined by measuring the distance from a floor or ceiling. Either way, you will know the center measurement of your existing pipe and the cen­ter measurement for where you want the offset pipe to comply with. Know­ing these two numbers will give you the Set figure. Remember, Set is meas­ured as the vertical distance between the centers of two pipes. Refer back to Fig. 2.1 if you need a reminder on this concept.

Let’s assume that you know what your Set distance is. You want to know what the Travel is. To do this, use the table in 2.5. For example, if you were looking for the Travel of a 45° offset when the Set is known, you would mul­tiply the Set measurement by a factor of 1.414. Now, let’s assume that you know the Travel and want to know the Set. For the same 45° offset, you would multiply the Travel measurement by.707. It’s really simple, as long you have the chart to use. The procedure is the same for different degrees of offset. Just refer to the chart and you will find your answers quickly and easily.

FIGURE 2.5 ■ Multipliers for calculating simple offsets.

Finding Run measurements is no more difficult than Set or Travel. Say you have the Set measurement and want to know the Run figure for a 45° off­set. Multiply the Set figure by 1.000 to get the Run number. If you are work­ing with the Travel number, multiply that number by.707 to get the Run number for a 45° offset.