Deterministic waste-load allocation model. Although any number of pollutants may be considered in the overall quality management of a river system, in this example, application a biochemical oxygen demand-dissolved oxygen (BOD-DO) water-quality model is considered.

In LP format, the deterministic WLA model considered herein can be written as

N

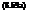Maximize ^^( Bj + Dj)

j=i

subject to

1. Constraints on water quality:

aoi + ®ij Bj + ^ ttij Dj < DOsat – DOfd for i = 1,2,…, M (8.59b)

j=1 j=1

2.

Constraints on treatment equity:

3. Constraints on treatment efficiency:

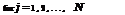
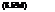Bj

e-j < 1 – T <e j

j

where Bj, Dj, and Ij are the effluent waste concentrations (mg/L BOD), ef­fluent DO deficit concentration (mg/L), and raw waste influent concentration (mg/L BOD) at discharge location j, respectively, and N is the total number of waste dischargers. The LHS coefficients aoi, ®ij, and Uij in Eq. (8.59b) are
the technological transfer coefficients relating impact on DO concentrations at downstream locations i resulting from the background waste and waste input at an upstream location j. These technological transfer coefficients are functions of water-quality parameters such as reaeration and deoxygenation rates, flow velocity, etc. DOistd and DOisat represent the required DO standard and saturated DO concentration at control point i, respectively. Finally, Ea is the allowable dif­ference (i. e., equity) in treatment efficiency between two waste dischargers, and e_j and e j are the lower and upper bounds of waste-removal efficiency for the j th discharger, respectively. The importance of incorporating the treatment equity in the WLA problems is discussed by many researchers (Gross, 1965; Loucks et al., 1967; Miller and Gill, 1976; Brill et al., 1976; Chadderton et al., 1981).

The water-quality constraint relating the response of DO to the effluent waste can be defined by water-quality models such as the Streeter-Phelps equation (Streeter and Phelps, 1925) or its variations (Dobbins, 1964; Krenkel and Novotny, 1980). To demonstrate the proposed methodologies, the original Streeter-Phelps equation is used herein to derive the water-quality constraints. Expressions for &ij and Uij, based on the Streeter-Phelps equation, are shown in Appendix 8A. The Streeter-Phelps equation for DO deficit is given as follows:

Dx = TKdL0, (e-KdX/U – e-K“x/U) + Doe-Kax/U (8.60)

where Dx is the DO deficit concentration (mg/L) at stream location x (mi), Kd is the deoxygenation coefficient for BOD (days-1), Ka is the reaeration-rate coefficient (days-1), L0 is the BOD concentration at the upstream end of the reach (that is, x = 0), D0 is the DO deficit concentration at the upstream end of the reach, and U is the average streamflow velocity in the reach (mi/day).

Chance-constrained waste-load allocation model. The deterministic WLA model presented in Eqs. (8.59a-d) serves as the basic model for deriving the stochastic WLA model. Considering the existence of uncertainty within the stream envi­ronment, the water-quality constraints given by Eq. (8.59b) can be expressed probabilistically as

Пі Пі j

aoi + X) ©ij Bj + 53 Uij Dj < DOsat – DOfd> ai for і = 1,2,…, M

j=1 j=1 )

(8.61)

Based on Eq. (8.53), the deterministic equivalent of Eq. (8.60) can be derived as

(8.62)

in which Ri = DOSat – DOfd – E(a0i), (B, D) is the column vector of BOD and DO deficit concentrations in waste effluent, and C (©i, Qi) is the covariance matrix associated with the technological transfer coefficients in the ith water – quality constraint, including a0i. The stochastic WLA model to be solved consists of Eqs. (8.58a), (8.62), (8.58c), and (8.58d).

Assessments of statistical properties of random technological coefficients. To solve the stochastic WLA model, it is necessary to assess the statistical properties of the random LHS in the chance-constraint Eq. (8.62). As shown in Appendix 8A, the technological transfer coefficients &ij and Uij are nonlinear functions of the stochastic water-quality parameters that are cross-correlated among them within each stream reach and spatially correlated between stream reaches. Furthermore, the complexities of the functional relationships between these transfer coefficients and the water-quality parameters increases rapidly as the control point moves downstream. Hence the analytical derivation of the statistical properties of &ij and Uij becomes a formidable task given even a small number of reaches. As a practical alternative, simulation procedures may be used to estimate the mean and covariance structure of the random techno­logical coefficients within a given water-quality constraint.

The assumptions made in the Monte Carlo simulation to generate water – quality parameters in all reaches of the stream system are as follows: (1) The representative values for the reaeration coefficient, deoxygenation coefficient, and average flow velocity in each reach are second-order stationary; i. e., the spatial covariance functions of water quality-parameters are dependent only on the “space lag” or separation distance; (2) correlation between the reaeration coefficient and average flow velocity exists only within the same stream reach; (3) background DO and BOD concentrations at the upstream end of the entire stream system are independent of each other and of all other water-quality parameters; and (4) all water-quality parameters follow a normal distribution.

In the simulation, variance-covariance matrices representing the spatial cor­relation of a water-quality parameter can be derived from the variogram models (Journel and Huijbregts, 1978) in the field of geostatistics. Three commonly used variogram models are:

1. Transitive variogram model:

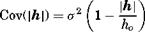(8.63)

2. Spherical variogram model:

(8.64)

3.

Gaussian variogram model:

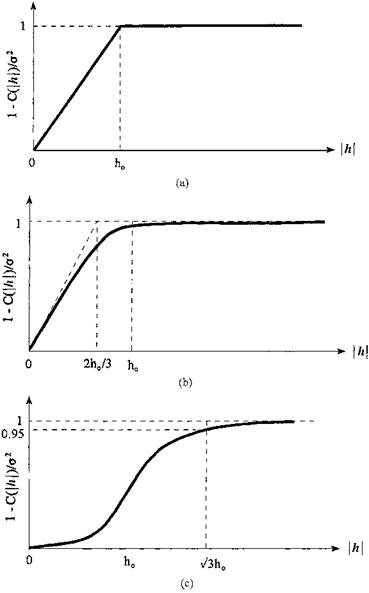
in which Cov(|h|) represents the value of covariance between two measure­ments of the same water-quality parameter separated by a distance h | apart, ho is the length of zone of influence, and a2 is the variance of the water – quality parameter within a given reach. The value of correlation coefficient p(|h|) can be calculated as p(|h|) = Cov(|h|)/a2. When the distance between reaches exceeds ho, the value of the covariance function goes to zero, and the corresponding correlation coefficient is zero as well. Graphically, the three variogram models are shown in Fig. 8.18.

To illustrate the concept, consider the water-quality parameters’ reaeration coefficient Ka and average flow velocity U. From the variogram models, the correlation matrix for the two parameters can be constructed as follows:

in which Ka = (Ka, i, Ka2,…, Ka N) and U = (Ui, U2,…, UN) are vectors of the reaeration coefficient and average velocity in each stream reach, respec­tively (see Fig. 8.19). In Eq. (8.66), R(Ka, Ka), R(Ka, U), R(U, U) are N x N square symmetric correlation matrices, with N being the number of stream reaches in the WLA model. Submatrices R(Ka, Ka) and R(U, U) define the spa­tial correlation of Ka and U between the reaches, whereas submatrix R(Ka, U) defines the cross-correlation between Ka and U within the same reach. Under assumption 2 previously mentioned, the submatrix R(Ka, U) is a diagonal ma­trix. For water-quality parameters that are not cross-correlated with other pa­rameters but are spatially correlated, the associated correlation matrix has a form similar to R(U, U). For parameters that are spatially independent, their correlation matrices are in the form of an identify matrix. Once the correlation matrix of normal stochastic parameters within a reach and between reaches is established according to the specified variogram model, generation of stochastic water-quality parameters can be obtained easily by the procedures for gener­ating multivariate random variates described in Sec. 7.5.2.

In summary, the simulation for generating spatially and cross-correlated water-quality parameters can be outlined as the follows:

1. Select an appropriate variogram model for a given water-quality parameter, and construct the corresponding covariance matrix C or correlation matrix R.

2. Apply procedures described in Sec. 7.5.2 to obtain the values of the water – quality parameter for each reach in the WLA model.

3. Repeat steps 1 and 2 for all water-quality parameters.

For each set of the water-quality parameters generated by steps 1 through 3, the values of the technological coefficients are computed. Based on the simu­lated values, the mean and covariance matrices of the random technological coefficients for each water-quality constraint are calculated and used in solving the stochastic WLA problem. The simulation procedure described in this sub­section to account for spatial correlation is called unconditional simulation in the field of geostatistics (Journel and Huijbregts, 1978).

Technique for solving an optimal stochastic WLA model. The deterministic WLA model presented previously follows an LP format and can be solved using the simplex algorithm. However, the deterministic equivalents of the chance – constrained water-quality constraints are nonlinear. Thus the problem is one of nonlinear optimization, which can be solved by various nonlinear programming techniques mentioned in Sec. 8.1.2.

In this example, linearization of the chance-constrained water-quality constraints is done, and the linearized model is solved iteratively using the LP simplex technique. More specifically, the algorithm selects an assumed solution to the stochastic WLA model that is used to calculate the value of the nonlinear terms in Eq. (8.62). The nonlinear terms then become constants and are moved to the RHS of the constraints. The resulting linearized water-quality constraints can be written as

E(®ij)Bj + E(Qij)Dj < Щ – F-1(at) (B, t»tC(&t, )(B, D)

j=1 J =1

(8.67)

in which B and D are assumed solution vectors to the stochastic WLA model.

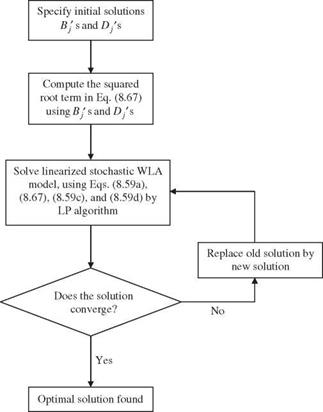
The linearized stochastic WLA model, replacing Eq. (8.62) by Eq. (8.67), can be solved using LP techniques repeatedly, each time updating the previous

solution values with those obtained from the current iteration, resulting in new values for the RHS. The procedure is repeated until convergence criteria are met between any two successive iterations. A flowchart depicting the procedures is given in Fig. 8.20. Of course, alternative stopping rules could be incorporated in the algorithm to prevent excessive iteration during the computation. Prior to the application of these solution procedures, an assumption for the distribution of the random LHS must be made to determine the appropriate value for the term Fz(ai) in Eq. (8.67).

Owing to the nonlinear nature of the stochastic WLA model, the global op­timum solution, in general, cannot be guaranteed. It is suggested that a few runs of the solution procedure with different initial solutions be carried out to ensure that the model solution converges to the overall optimum. A reasonable initial solution is to select the waste effluent concentration for each discharger associated with the upper bounds of their respective treatment levels. By doing so, the initial solution corresponds to waste discharge at their respective lower

limits. If the stochastic WLA solution is infeasible during the first iteration, it is likely that the feasible solution to the stochastic WLA problem does not exist. Hence time and computational effort could be saved in searching for an optimal solution that might not exist.

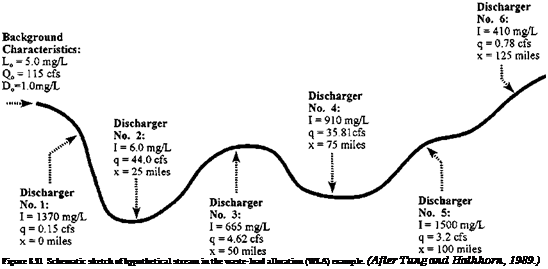
Numerical example. The preceding chance-constrained WLA model is applied to a six-reach example shown in Fig. 8.21. The means and standard deviations for the water-quality parameters in each reach are given in Tables 8.5 and 8.6 based on the data reported in the literature (Churchill et al., 1962; Chadderton et al., 1982; Zielinski, 1988).

To assess the mean and correlation matrix of the random technological co­efficients in the water-quality constraints, the Monte Carlo simulation proce­dure described in Sec. 6.5.2 is implemented to generate multivariate normal water-quality parameters. Different numbers of simulation sets are generated to examine the stability of the resulting means and covariance matrix of the technological coefficients. It was found that the statistical properties of ©ij and Uij become stable using 200 sets of simulated parameters. In the exam­ple, a positive correlation coefficient of 0.8 between the reaeration coefficient and average flow velocity is used. Both normal and lognormal distributions are assumed for the random LHS of the water-quality constraints

Пі Пі

a0i + 53 ©i> + 53 ^ij Dj (8.68)

j=1 j=1

in Eq. (8.67). Various reliability levels ai ranging from 0.85 to 0.99 for the water-quality constraints are considered.

In the example, the length of each reach in the system is 10 mi, and the spatial correlation of representative water-quality parameter values between two reaches is computed based on the separation distance between the centers of the two reaches. To examine the effect of spatial correlation structure on the optimal waste-load allocation, two zones of influence (ho = 15 mi and ho = 30 mi) along with the three variogram models, Eqs. (8.63) through (8.65), are used. A value of ho = 15 mi implies that the water-quality parameters in a given reach are spatially correlated only with the two immediate adjacent reaches. For ho = 30 mi, the spatial correlation extends two reaches upstream and downstream of the reach under consideration. The optimal solutions to the stochastic WLA problem under these various conditions are presented in Tables

8.7 and 8.8.

Examining Tables 8.7 and 8.8, the maximum total BOD discharge, under a given spatial correlation structure, reduces as the reliability of water-quality constraints increases. This behavior is expected because an increase in water – quality compliance reliability is equivalent to imposing stricter standards on water-quality assurance. To meet this increased water-quality compliance re­liability, the amount of waste discharge must be reduced to lower the risk of water-quality violation at the various control points. When continuing to in­crease the required reliability for the water-quality constraints, at some point these restrictions could become too stringent, and feasible solutions to the prob­lem are no longer obtainable.

From Tables 8.7 and 8.8, using a lognormal distribution for the LHS of water – quality constraints yields a higher total BOD discharge than that under a nor­mal distribution when the performance reliability requirement is 0.85. How­ever, the results reverse themselves when reliability requirements are greater than or equal to 0.90. This indicates that the optimal solution to the stochastic WLA model depends on the distribution used for the LHS of the water-quality constraints. From the investigation of Tung and Hathhorn (1989), a lognor­mal distribution was found to best describe the DO deficit concentration in a single-reach case. In other words, each term of the LHS in the water-quality

constraints could be considered as a lognormal random variable. Therefore, the LHS is the sum of correlated lognormal random variables. For the first two or three reaches from the upstream end of the system, the distribution of the LHS may close to lognormal because the number of terms in the LHS is few. How­ever, considering the control point for farther-downstream reaches, the number of terms in the LHS increases, and the resulting distribution may approach to normal from the argument of the central limit theorem. Since the true distribu­tion for the LHS of water-quality constraints is not known, it is suggested that different distributions be used for model solutions and that the least amount of total BOD load be applied for implementation.

Furthermore, the impacts of the extent of the spatial correlation of the water – quality parameters (represented by the length of ho) and the structure (repre­sented by the form of the variogram) on the results of the stochastic WLA model also can be observed. When ho = 15 mi, where the spatial correlation of the water-quality parameters extends only one reach, the maximum allowable total BOD load, for all three variogram models, is higher than that of spatially independent case. When the spatial correlation extends over two reaches (that is, ho = 30 mi), use of transitive and spherical variogram models results in lower maximum total BOD loads than that of the spatially independent case, whereas use of a Gaussian variogram yields a higher total BOD load. The model results using a transitive variogram are very similar to those of a spherical model.

As a final comment on the computational aspects of the proposed technique for solving the stochastic nonlinear WLA model formulated in this study, it was observed that the iterative technique proposed takes three to five iterations to converge for all the cases investigated. Therefore, the proposed solution proce­dure is quite efficient in solving the stochastic WLA model.