Reliability of Simple Systems
In this section the reliability of some simple systems will be discussed. In the framework of time-to-failure analysis, availability of such systems will be presented. Information such as this is essential to serve as the building blocks for determination of reliability or availability of more complex systems.
A series system requires that all its components or modes of operation perform satisfactorily to ensure a satisfactory operation of the entire system. In the context of load-resistance interference, the failure event associated with a mode of operation is
Fm = {Wm < 0} form = 1, 2,…, M
in which Wm is the random performance variable associated with the mth mode of operation. Referring to Chap. 4, the failure probability and reliability associated with the mth mode of operation, respectively, are
P (Fm) = P ( Wm < 0) = P (Zm < ~Pm) = ®(-fim) (7.28a)
P (Fm) = P ( Wm > 0) = P (Zm > – Pm) = 4Pm) (7.28b)
in which Zm is the standard normal random variable associated with Wm, and pm is the reliability index associated with the mth mode of operation.
The failure probability of a series system involving M modes of operation, according to Eq. (7.1), can be expressed as
|
|||||||||
|
|
|
|
|
|||||

Because all the standardized normal random variables Zm’s generally are correlated, computation of the exact system failure probability using Eq. (7.29) may not be practical, especially when the number of modes of operation M is large. For this case, the second-order bounds for Pf, sys could be viable. According to Eq. (7.26), the bounds for system failure probability are
in which Ф(—вj, —em I Pjm) is the bivariate normal probability, which can be computed by procedures described in Sec. 2.7.2, with Pjm being the correlation coefficient between the performance variables Wj and Wm for the j th and mth modes of operation. Accordingly, the bounds on reliability of a series system can be obtained easily by using Eq. (7.11b).
Although computation of the exact bivariate normal probability can be obtained through numerical integration, sometimes information about its bounds is sufficient. Under a positively correlated case, narrow bounds of Ф(—вj, —em I Pjm > 0) that require evaluations of only univariate normal probabilities are
where ві Im = в, Ртв" (7.32a)
v/irpm
emu = em,— P’"’m’ (7.32b)
j
In the case that the pair of performance functions is negatively correlated, the bounds for joint failure probability are
0 < Ф(— Єі, —em I Pjm < 0) < minm—emm—ej | m), Ф( — в} m—em | j )] (7.33)
The derivations of Eqs.(7.31) and (7.33) are given in Appendix 7A. Ang and Tang (1984) pointed out that use of an approximation of Eq. (7.31) could improve (tighten) the second-order bound of Eq. (7.30) when the single-mode failure probabilities are small, say, on the order of 10—4. However, if the single-mode
failure probabilities are all large (e. g., 10-2), the bound of Eq. (7.31) will be wide.
In fact, the reliability of a series system can be computed, according to Eq. (7.2), as
It should be pointed out that, in general, P [n(Zm > —em)] = P [n(Zm < fim)] unless for the univariate case. As can be seen, the reliability of a series system is the multivariate normal probability whose determination can be made by Ditlevsen’s approach, described in Sec. 2.7.2, or by various bounding approaches discussed in Sec. 2.7.3.
Example 7.6 Consider a system consisting of three modes of operation, each of which is specified by the following linear performance functions:
W1( X) = X1 + 2 X2
W2( X) = X1 + X2 + X3
W3( X) = X2 + 2X3
in which the stochastic basic variables X1, X2, and X3 are multivariate normal random variables with the vector of means
Vx = (М1, М2, М3/ = (6, 6, 6/
and covariance matrix
|
■9.00 |
0.00 |
0.00 |
|
|
Cx = |
0.00 |
9.00 |
0.00 |
|
.0.00 |
0.00 |
9.00 |
The state of the system is such that if any of the three modes of operation fail, the system would fail. Calculate the system reliability.
Solution From the preceding covariance matrix Cx, it is understood that all three stochastic basic variables are uncorrelated, each with a variance of 9, that is, Var(X1) = Var(X2) = Var(X3) = 9. The vector of expected values of W1, W2, and W3 is
Vw = (Mw1, Mw2, Mw3) = [6 + 2(6), 6 + 6 + 6, 6 + 2(6)/ = (18, 18, 18/
The covariance matrix of the three performance functions W’s can be computed as
Cw = S1 Cx S
in which S, the sensitivity matrix, is an K x M matrix, with M and K being the number of performance functions and stochastic basic variables, respectively. The sensitivity matrix S contains, in each column, the vector of sensitivity coefficients for each performance function with respect to individual stochastic basic variable, that is,
S = [S1, 82,…, sm ]
for m = 1,2,…, M. In this example, since all performance functions are linear, the sensitivity matrix consists of coefficients in the performance functions, that is,
|
1 |
2 |
0 |
|
|
s1 = |
1 |
1 |
1 |
|
1 0 |
1 |
to 1 |
Hence the covariance matrix of the three performance functions can be obtained as
|
45 |
27 |
18 |
|
|
Cw = |
27 |
27 |
27 |
|
18 |
27 |
45 |
As can be seen, even though the three stochastic basic variables are uncorrelated, the three performance functions are correlated because they are defined by some stochastic basic variables common to the other performance functions. Hence the variances of W1, W2, and W3 appear on the diagonal of Cw, namely,
Var( W1) = 45 Var( W2) = 27 and Var( W3) = 47
The corresponding correlation matrix of random W’s can be obtained easily as
‘1.000 0.7746 0.4000’
![]()
![]()
0.7746 1.000 0.7746
0.4000 0.7746 1.000
The system failure probability is defined as
pf ,sys = P [(W1 < 0) U (W2 < 0) U (W3 < 0)]
= P [(Z1 < -2.68) U (Z2 < -3.46) U (Z3 < -2.68)]
The exact system failure probability can be obtained as pf sys = P [(Z1 < -2.68) U (Z2 < -3.46) U (Z3 < -2.68)]
= [P(Z1 < -2.68) + P(Z2 < -3.46) + P(Z3 < -2.68)]
– [P(Z1 < -2.68, Z2 < -3.46) + P(Z1 < -2.68, Z3 < -2.68)
+ P(Z2 < -3.46, Z3 < -2.68)] + P(Z1 < -2.68, Z2 < -3.46, Z3 < -2.68)
= (0.003681 + 0.0002701 + 0.003681) – (0.0001659 + 0.0001987 + 0.0001659) + 0.0001556 = 0.0072572
Hence the system reliability ps>sys = 1 – 0.0072572 = 0.9927428. Note that the preceding bivariate normal probabilities are calculated by Eq. (2.121), whereas the trivariate normal probability is computed according to Ditlevsen’s algorithm using Taylor expansion described in Sec. 2.7.2.
Alternatively, the second-order bounds for the system failure probability can be computed according to Eq. (7.30). The results are
0.007102 < pf, sys < 0.007268
and the corresponding bounds on the system reliability ps, sys are
0.992732 < ps, sys < 0.992898
In the framework of time-to-failure analysis, the reliability ps, m(t) and failure probability pf, m(t) of the mth component over the time interval (0, t ], according to Eqs. (5.1a) and (5.1b), are
|
/ |
TO
fm(r) dr (7.35a)
and P(Fm) = pf, m(t) — [ fт(т)dx (7.35b)
70
respectively, where f m(t) is the failure density function for the mth component.
In the case that the performance of individual components is independent of each other, the reliability of a series system is
Similarly, the availability of a series system involving M independent components is
M
Asys(t) — Ц Am(t) (7.37)
m—1
in which Aeys(t) and Am(t) are availabilities of the entire system and the mth component, respectively, at time t.
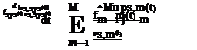 |
||||
According to Eqs. (5.2) and (5.3), the failure density function f sys(t) and the failure rate hsys(t) for a series system involving M independent components can be derived, respectively, as
For the special case of an exponential failure density function such as
 for t > 0, Xm > 0, m — 1,2,…, M
for t > 0, Xm > 0, m — 1,2,…, M
the reliability and unreliability of a series system with M independent components, respectively, are
Assuming an exponential repair function for each independent component, the availability and unavailability for a series system, according to Eqs. (7.37) and (5.59), are
![]() and Usys(t) — 1 Asys(t)
and Usys(t) — 1 Asys(t)
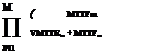 |
|||
in which nm is the constant repair rate for the mth component, and Usys(t) is the system unavailability at time t. The stationary system availability, by Eq. (5.60), can be expressed as
in which MTTRm and MTTFm are, respectively, the mean time to repair and mean time to failure of the mth component.
Example 7.7 As an example of a series system, consider a pumping station consisting of two different pumps in series, both of which must operate to pump the required quantity. The constant failure rates for the pumps are Л1 = 0.0003 failures/h and Л2 = 0.0002 failures/h. For a 2000-h mission time, the system reliability, according to Eq. (7.40a), is
ps, sys(t = 2000) = exp[-(0.0003 + 0.0002)(2000)] = 0.90484 and the MTTF of the system is






Leave a reply